A lineáris egyenletrendszer kompatibilitási feltétele. A Kronecker-Capelli tétel. Lineáris algebrai egyenletrendszerek megoldása, megoldási módszerek, példák Egy egyenletnek végtelen számú megoldása van, ha

Rendszer m lineáris egyenletek n ismeretlennel formarendszernek nevezzük

Ahol aijÉs b i (én=1,…,m; b=1,…,n) néhány ismert szám, és x 1,…,x n- ismeretlen. Az együtthatók jelölésében aij első index én jelöli az egyenlet számát, a másodikat j az ismeretlen száma, amelyen ez az együttható áll.

Az ismeretlenekre vonatkozó együtthatók mátrix formájában lesznek felírva , amit hívni fogunk rendszermátrix.

Az egyenletek jobb oldalán található számok b 1 ,…,b m hívott ingyenes tagok.

Összesített n számok c 1 ,…,c n hívott döntés ennek a rendszernek, ha a rendszer minden egyenlete egyenlőséggé válik, miután számokat helyettesítünk bele c 1 ,…,c n a megfelelő ismeretlenek helyett x 1,…,x n.

A mi feladatunk az lesz, hogy megoldásokat találjunk a rendszerre. Ebben az esetben három helyzet állhat elő:

Olyan lineáris egyenletrendszert nevezünk, amelynek legalább egy megoldása van közös. Ellenkező esetben pl. ha a rendszernek nincsenek megoldásai, akkor ún összeegyeztethetetlen.

Fontolja meg, hogyan találhat megoldást a rendszerre.

MÁTRIX MÓDSZER LINEÁRIS EGYENLETRENDSZER MEGOLDÁSÁRA

A mátrixok lehetővé teszik egy lineáris egyenletrendszer rövid leírását. Adjunk meg egy három egyenletrendszert három ismeretlennel:

Tekintsük a rendszer mátrixát 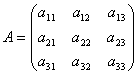valamint ismeretlen és szabad tagok mátrixoszlopai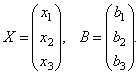

Keressük meg a terméket

azok. a szorzat eredményeként megkapjuk ennek a rendszernek az egyenleteinek bal oldalát. Ekkor a mátrixegyenlőség definícióját használva ez a rendszer így írható fel

vagy rövidebb A∙X=B.

Itt a mátrixok AÉs B ismertek, és a mátrix x ismeretlen. Meg kell találni, mert. elemei ennek a rendszernek a megoldása. Ezt az egyenletet ún mátrix egyenlet.

Legyen a mátrix determináns különbözik nullától | A| ≠ 0. Ekkor a mátrixegyenletet a következőképpen oldjuk meg. Szorozzuk meg a bal oldali egyenlet mindkét oldalát a mátrixszal A-1, a mátrix inverze A: . Mert a A -1 A = EÉs E∙X=X, akkor a mátrixegyenlet megoldását a formában kapjuk meg X = A -1 B .

Megjegyzendő, hogy mivel az inverz mátrix csak négyzetes mátrixokra található, a mátrixmódszer csak azokat a rendszereket tudja megoldani, amelyekben az egyenletek száma megegyezik az ismeretlenek számával. A rendszer mátrixos jelölése azonban lehetséges abban az esetben is, ha az egyenletek száma nem egyenlő az ismeretlenek számával, akkor a mátrix A nem négyzet alakú, és ezért lehetetlen megoldást találni a rendszerre a formában X = A -1 B.

Példák. Egyenletrendszerek megoldása.

CRAMER SZABÁLYA

Tekintsünk egy 3 lineáris egyenletrendszert három ismeretlennel:

A rendszer mátrixának megfelelő harmadrendű determináns, azaz. ismeretlenek együtthatóiból áll,

hívott rendszer meghatározó.

További három determinánst állítunk össze a következőképpen: a D determinánsban egymás után 1, 2 és 3 oszlopot cserélünk szabad tagokból álló oszlopra.

Ekkor a következő eredményt tudjuk bizonyítani.

Tétel (Cramer-szabály). Ha a rendszer determinánsa Δ ≠ 0, akkor a vizsgált rendszernek csak egy megoldása van, és

Bizonyíték. Tehát vegyünk egy három egyenletből álló rendszert három ismeretlennel. Szorozzuk meg a rendszer 1. egyenletét az algebrai komplementerrel A 11 elem egy 11, 2. egyenlet - be A21és 3. - on A 31:

Adjuk hozzá ezeket az egyenleteket:

Tekintsük ennek az egyenletnek mindegyik zárójelét és jobb oldalát. A determináns 1. oszlop elemei szerinti kiterjesztésének tételével

Hasonlóképpen kimutatható, hogy és .

Végül is ezt könnyű belátni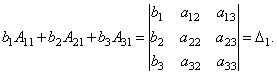

Így megkapjuk az egyenlőséget: .

Ennélfogva, .

A és egyenlőségeket hasonlóan származtatjuk, ahonnan a tétel állítása következik.

Így megjegyezzük, hogy ha a rendszer determinánsa Δ ≠ 0, akkor a rendszernek egyedi megoldása van, és fordítva. Ha a rendszer determinánsa egyenlő nullával, akkor a rendszernek vagy végtelen megoldáshalmaza van, vagy nincs megoldása, pl. összeegyeztethetetlen.

Példák. Egyenletrendszer megoldása

GAUSS MÓDSZER

A korábban vizsgált módszerekkel csak azokat a rendszereket lehet megoldani, amelyekben az egyenletek száma egybeesik az ismeretlenek számával, és a rendszer determinánsának nullától eltérőnek kell lennie. A Gauss-módszer univerzálisabb, és tetszőleges számú egyenletű rendszerekhez alkalmas. Ez abból áll, hogy a rendszer egyenleteiből egymást követően ki kell zárni az ismeretleneket.

Tekintsünk ismét egy három egyenletrendszert három ismeretlennel:

Az elsõ egyenletet változatlanul hagyjuk, a 2. és 3. egyenletbõl pedig kizárjuk a tartalmazó kifejezéseket x 1. Ehhez elosztjuk a második egyenletet A 21 és szorozzuk meg - A 11, majd add össze az 1. egyenlettel. Hasonlóképpen felosztjuk a harmadik egyenletet is A 31 és szorozzuk meg - A 11, majd add hozzá az elsőhöz. Ennek eredményeként az eredeti rendszer a következő formában lesz:

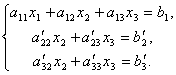
Most az utolsó egyenletből kiküszöböljük a tartalmazó kifejezést x2. Ehhez osszuk el a harmadik egyenletet -vel, szorozzuk meg és adjuk hozzá a másodikhoz. Ekkor lesz egy egyenletrendszerünk:

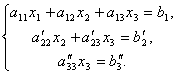
Ezért az utolsó egyenletből könnyű megtalálni x 3, majd a 2. egyenletből x2és végül 1-től - x 1.

A Gauss-módszer alkalmazásakor az egyenletek szükség esetén felcserélhetők.

Gyakran írás helyett új rendszer az egyenletek a rendszer kiterjesztett mátrixának kiírására korlátozódnak:

majd elemi transzformációk segítségével hozza háromszög vagy átló formába.

NAK NEK elemi átalakulások A mátrixok a következő transzformációkat tartalmazzák:

sorok vagy oszlopok permutációja;
egy karakterlánc szorzása nullától eltérő számmal;
egy sorhoz további sorokat ad.

Példák: Egyenletrendszerek megoldása Gauss módszerrel.

Így a rendszernek végtelen számú megoldása van.

8. fejezet

8.2. Két lineáris egyenletrendszer két ismeretlennel

Meghatározás

Több olyan egyenletet nevezünk, amelyben az azonos nevű ismeretlenek ugyanazt a mennyiséget jelölik egyenletrendszer.
A nézetrendszert ún normál forma két lineáris egyenletrendszer két ismeretlennel.
Egy ilyen rendszer megoldása azt jelenti, hogy mindkét egyenletre megtaláljuk az összes közös megoldás halmazát.

De hogyan lehet megoldani egy ilyen rendszert?

Egy ilyen rendszer például grafikusan is megoldható. Általában egy ilyen rendszert grafikusan két egyenes ábrázol, és ezen egyenletek általános megoldása (a rendszer megoldása) a két egyenes közös pontjának koordinátái lesznek. Itt három eset lehetséges:
1) Az egyeneseknek (grafikonoknak) csak egy közös pontja van (metszéspontja) - az egyenletrendszernek egyedi megoldása van, és határozottnak nevezik.
2) Az egyeneseknek (grafikonoknak) nincs közös pontja (párhuzamos) - a rendszernek nincs megoldása, és inkonzisztensnek nevezik.
3) Az egyeneseknek (grafikonoknak) végtelen sok közös pontja van (egybeesik) - a rendszernek végtelen számú megoldása van, és határozatlannak nevezik.

Valamit még nem értek. Talán példákkal világosabb lesz?

Természetesen most minden esetre adunk egy példát, és minden azonnal világosabb lesz.

Kezdjük egy példával, amikor a rendszer határozott (egyedi megoldása van). Vegyük a rendszert. Ezekről a függvényekről grafikonokat készítünk.

Csak egy pontban metszik egymást, ezért ennek a rendszernek a megoldása csak a pont koordinátái: , .

Most példát adunk egy inkonzisztens rendszerre (amelynek nincs megoldása). Tekintsünk egy ilyen rendszert.

Ebben az esetben a rendszer inkonzisztens: a bal oldali részek egyenlőek, míg a jobb oldali részek eltérőek. A grafikonoknak nincs közös pontja (párhuzamos), ezért a rendszernek nincs megoldása.

Nos, most az utolsó eset marad, amikor a rendszer határozatlan (végtelen számú megoldása van). Íme egy példa egy ilyen rendszerre: . Ábrázoljuk ezen egyenletek grafikonjait.

Az egyeneseknek (gráfoknak) végtelen sok közös pontja van (egybeesik), ami azt jelenti, hogy a rendszernek végtelen számú megoldása van. Ebben az esetben a rendszer egyenletei ekvivalensek (a második egyenletet megszorozzuk 2 , megkapjuk az első egyenletet).

A legfontosabb az első eset. Az egyetlen megoldás egy ilyen rendszerre mindig grafikusan található - néha pontosan, és legtöbbször hozzávetőlegesen a szükséges pontossággal.

Meghatározás

Két egyenletrendszert nevezünk ekvivalensnek (egyenértékű), ha mindegyik megoldása a másiknak is megoldása (a megoldáshalmazok megegyeznek), vagy ha mindkettőnek nincs megoldása.

Lineáris agebrai egyenletrendszer (SLAE) kompatibilitási rendszerének vizsgálata azt jelenti, hogy meg kell találni, hogy ennek a rendszernek vannak-e megoldásai vagy sem. Nos, ha vannak megoldások, akkor jelezze, hogy hány.

Információkra lesz szükségünk a "Lineáris algebrai egyenletrendszer. Alapfogalmak. Mátrix jelölés" témakörből. Különösen olyan fogalmakra van szükség, mint a rendszer mátrixa és a rendszer kiterjesztett mátrixa, mivel a Kronecker-Capelli tétel megfogalmazása ezeken alapul. Szokás szerint a rendszer mátrixát a $A$, a kiterjesztett rendszer mátrixát pedig a $\widetilde(A)$ betűvel jelöljük.

Kronecker-Capelli tétel

Egy lineáris algebrai egyenletrendszer akkor és csak akkor konzisztens, ha a rendszer mátrixának rangja egyenlő a rendszer kiterjesztett mátrixának rangjával, azaz. $\rank A=\rang\widetilde(A)$.

Hadd emlékeztesselek arra, hogy egy rendszert akkor nevezünk kötésnek, ha van legalább egy megoldása. A Kronecker-Capelli tétel ezt mondja: ha $\rang A=\rang\widetilde(A)$, akkor van megoldás; ha $\rang A\neq\rang\widetilde(A)$, akkor ennek a SLAE-nek nincs megoldása (inkonzisztens). A megoldások számára vonatkozó kérdésre a Kronecker-Capelli-tétel következménye adja meg a választ. A következmény utasítása a $n$ betűt használja, amely megegyezik az adott SLAE változóinak számával.

Következmény a Kronecker-Capelli tételből

Ha $\rang A\neq\rang\widetilde(A)$, akkor a SLAE inkonzisztens (nincs megoldása).
Ha $\rang A=\rang\widetilde(A)< n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
Ha $\rang A=\rang\widetilde(A) = n$, akkor az SLAE határozott (pontosan egy megoldása van).

Megjegyzendő, hogy a megfogalmazott tétel és annak következményei nem jelzik, hogyan találjuk meg az SLAE megoldását. Segítségükkel csak azt lehet megtudni, hogy ezek a megoldások léteznek-e vagy sem, és ha vannak, akkor hányan.

1. példa

SLAE felfedezése $ \left \(\begin(aligned) & -3x_1+9x_2-7x_3=17;\\ & -x_1+2x_2-4x_3=9;\\ & 4x_1-2x_2+19x_3=-42. \end(aligned) )\right.$ a konzisztencia érdekében Ha az SLAE konzisztens, adja meg a megoldások számát.

Egy adott SLAE megoldásának megtudásához a Kronecker-Capelli tételt használjuk. Szükségünk van a $A$ rendszer mátrixára és a $\widetilde(A)$ rendszer kiterjesztett mátrixára, ezeket írjuk fel:

$$ A=\left(\begin(tömb) (cccc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \end(array) \right);\; \widetilde(A)=\left(\begin(tömb) (cccc|c) -3 & 9 &-7 & 17 \\ -1 & 2 & -4 & 9\\ 4 & -2 & 19 & -42 \end(tömb)\jobbra). $$

Meg kell találnunk a következőt: $\rang A$ és $\rang\widetilde(A)$. Ennek számos módja van, amelyek közül néhányat a Mátrix Rank szakaszban találunk. Általában két módszert használnak az ilyen rendszerek tanulmányozására: "A mátrix rangjának kiszámítása definíció szerint" vagy "A mátrix rangjának kiszámítása elemi transzformációk módszerével".

1. számú módszer. A rangok számítása definíció szerint.

A definíció szerint a rang a mátrix minorjainak legmagasabb rendje, amelyek között van legalább egy nullától eltérő. Általában a vizsgálat az elsőrendű mollokkal kezdődik, de itt kényelmesebb azonnal folytatni a $A$ mátrix harmadrendű molljának kiszámítását. A harmadrendű moll elemei a vizsgált mátrix három sorának és három oszlopának metszéspontjában helyezkednek el. Mivel az $A$ mátrix csak 3 sort és 3 oszlopot tartalmaz, ezért az $A$ mátrix harmadrendű minora a $A$ mátrix determinánsa, azaz. $\DeltaA$. A determináns kiszámításához a "Képletek másod- és harmadrendű determinánsok kiszámításához" témakör 2. képletét alkalmazzuk:

$$ \Delta A=\left| \begin(tömb) (cc) -3 & 9 & -7 \\ -1 & 2 & -4 \\ 4 & -2 & 19 \end(tömb) \right|=-21. $$

Tehát van a $A$ mátrix harmadrendű mollja, amely nem egyenlő nullával. Negyedrendű moll nem alkotható, mivel 4 sor és 4 oszlop szükséges, az $A$ mátrixnak pedig csak 3 sora és 3 oszlopa van. Tehát a $A$ mátrix molljainak legmagasabb rendje, amelyek között van legalább egy nem nulla, egyenlő 3-mal. Ezért $\rang A=3$.

Meg kell találnunk a $\rang\widetilde(A)$-t is. Nézzük meg a $\widetilde(A)$ mátrix szerkezetét. A $\widetilde(A)$ mátrixban a $\widetilde(A)$ sorig vannak a $A$ mátrix elemei, és azt találtuk, hogy $\Delta A\neq 0$. Ezért a $\widetilde(A)$ mátrixnak van egy harmadrendű minorja, amely nem egyenlő nullával. A $\widetilde(A)$ mátrix negyedrendű molljait nem tudjuk összeállítani, ezért a következő következtetést vonjuk le: $\rang\widetilde(A)=3$.

Mivel $\rang A=\rang\widetilde(A)$, a Kronecker-Capelli tétel szerint a rendszer konzisztens, i.e. van megoldása (legalább egy). A megoldások számának jelzéséhez figyelembe vesszük, hogy SLAE-nk 3 ismeretlent tartalmaz: $x_1$, $x_2$ és $x_3$. Mivel az ismeretlenek száma $n=3$, ezért következtetünk: $\rang A=\rang\widetilde(A)=n$, ezért a Kronecker-Capelli tétel következménye szerint a rendszer határozott, i.e. egyedi megoldása van.

Probléma megoldódott. Mik ennek a módszernek a hátrányai és előnyei? Először is beszéljünk a profikról. Először is csak egy meghatározó tényezőt kellett találnunk. Ezek után azonnal levontuk a következtetést a megoldások számáról. Általában a standard tipikus számításokban olyan egyenletrendszereket adnak meg, amelyek három ismeretlent tartalmaznak, és egyetlen megoldással rendelkeznek. Az ilyen rendszerekre ez a módszer nagyon kényelmes, mert előre tudjuk, hogy van megoldás (egyébként tipikus számításban nem lenne példa). Azok. csak meg kell mutatnunk, hogy a legtöbbre van megoldás gyors út. Másodszor, a rendszermátrix determinánsának (azaz $\Delta A$) számított értéke később jól fog jönni: amikor az adott rendszert Cramer módszerrel vagy az inverz mátrix segítségével kezdjük megoldani.

De definíció szerint a rangszámítási módszer nem kívánatos, ha a $A$ rendszermátrix téglalap alakú. Ebben az esetben jobb a második módszer alkalmazása, amelyet az alábbiakban tárgyalunk. Emellett, ha $\Delta A=0$, akkor nem fogunk tudni semmit mondani egy adott inhomogén SLAE megoldásainak számáról. Lehet, hogy a SLAE-nek végtelen számú megoldása van, vagy lehet, hogy egyik sem. Ha $\Delta A=0$, akkor további kutatásra van szükség, ami gyakran nehézkes.

Összegezve az elmondottakat, megjegyzem, hogy az első módszer jó azoknak az SLAE-knek, amelyek rendszermátrixa négyzet. Ugyanakkor maga az SLAE három vagy négy ismeretlent tartalmaz, és szabványos szabványos számításokból vagy vezérlési munkákból származik.

2. számú módszer. Rangsorszámítás elemi transzformációk módszerével.

Ezt a módszert a megfelelő témakörben ismertetjük részletesen. Kiszámoljuk a $\widetilde(A)$ mátrix rangját. Miért a $\widetilde(A)$ mátrixok és nem a $A$? A lényeg az, hogy az $A$ mátrix része a $\widetilde(A)$ mátrixnak, így a $\widetilde(A)$ mátrix rangjának kiszámításával egyidejűleg megtaláljuk a $A$ mátrix rangját is. .

\begin(aligned) &\widetilde(A) =\left(\begin(array) (ccc|c) -3 & 9 &-7 & 17 \\ -1 & 2 & -4 & 9\\ 4 & - 2 & 19 & -42 \end(array) \right) \rightarrow \left|\text(az első és a második sor felcserélése)\jobbra| \rightarrow \\ &\rightarrow \left(\begin(array) (ccc|c) -1 & 2 & -4 & 9 \\ -3 & 9 &-7 & 17\\ 4 & -2 & 19 & - 42 \end(array) \right) \begin(array) (l) \phantom(0) \\ r_2-3r_1\\ r_3+4r_1 \end(array) \rightarrow \left(\begin(array) (ccc| c) -1 & 2 & -4 & 9 \\ 0 & 3 &5 & -10\\ 0 & 6 & 3 & -6 \end(array) \right) \begin(array) (l) \phantom(0 ) \\ \phantom(0)\\ r_3-2r_2 \end(array)\rightarrow\\ &\rightarrow \left(\begin(array) (ccc|c) -1 & 2 & -4 & 9 \\ 0 & 3 &5 & -10\\ 0 & 0 & -7 & 14 \end(tömb) \jobbra) \end(igazított)

A $\widetilde(A)$ mátrixot lépcsőzetes formára redukáltuk. Az így kapott lépésmátrixnak három nem nulla sora van, így a rangja 3. Ezért a $\widetilde(A)$ mátrix rangja 3, azaz. $\rank\widetilde(A)=3$. A $\widetilde(A)$ mátrix elemeivel transzformációkat végezve egyidejűleg transzformáltuk a $A$ mátrix vonal előtti elemeit. A $A$ mátrix is lépcsőzetes: $\left(\begin(array) (ccc) -1 & 2 & -4 \\ 0 & 3 &5 \\ 0 & 0 & -7 \end(array) \ jobbra )$. Következtetés: az $A$ mátrix rangja is egyenlő 3-mal, azaz. $\rank A=3$.

Mivel $\rang A=\rang\widetilde(A)$, a Kronecker-Capelli tétel szerint a rendszer konzisztens, i.e. van megoldása. A megoldások számának jelzéséhez figyelembe vesszük, hogy SLAE-nk 3 ismeretlent tartalmaz: $x_1$, $x_2$ és $x_3$. Mivel az ismeretlenek száma $n=3$, ezért következtetünk: $\rang A=\rang\widetilde(A)=n$, ezért a Kronecker-Capelli tétel következményének megfelelően a rendszer definiált, i.e. egyedi megoldása van.

Milyen előnyei vannak a második módszernek? A fő előnye a sokoldalúság. Számunkra nem mindegy, hogy a rendszer mátrixa négyzetes-e vagy sem. Ezenkívül ténylegesen végrehajtottuk a Gauss-módszer transzformációit. Már csak néhány lépés van hátra, és megkaphatjuk ennek a SLAE-nek a megoldását. Őszintén szólva a második módot jobban szeretem, mint az elsőt, de a választás ízlés dolga.

Válasz: Az adott SLAE konzisztens és definiált.

2. példa

SLAE felfedezése $ \left\( \begin(aligned) & x_1-x_2+2x_3=-1;\\ & -x_1+2x_2-3x_3=3;\\ & 2x_1-x_2+3x_3=2;\\ & 3x_1- 2x_2+5x_3=1;\\ & 2x_1-3x_2+5x_3=-4.\end(igazított) \jobbra.$ a következetesség érdekében.

A rendszer mátrixának és kiterjesztett mátrixának sorait elemi transzformációk módszerével fogjuk megtalálni. Kibővített rendszermátrix: $\widetilde(A)=\left(\begin(array) (ccc|c) 1 & -1 & 2 & -1\\ -1 & 2 & -3 & 3 \\ 2 & -1 & 3 & 2 \\ 3 & -2 & 5 & 1 \\ 2 & -3 & 5 & -4 \end(array) \right)$. Keressük meg a szükséges rangokat a rendszer kiterjesztett mátrixának átalakításával:

$$ \left(\begin(array) (ccc|c) 1 & -1 & 2 & -1\\ -1 & 2 & -3 & 3 \\ 2 & -3 & 5 & -4 \\ 3 & -2 & 5 & 1 \\ 2 & -1 & 3 & 2 \end(tömb) \jobbra) \begin(tömb) (l) \fantom(0)\\r_2+r_1\\r_3-2r_1\\ r_4 -3r_1\\r_5-2r_1\end(tömb)\jobbra nyíl \left(\begin(tömb) (ccc|c) 1 & -1 & 2 & -1\\ 0 & 1 & -1 & 2 \\ 0 & -1 & 1 & -2 \\ 0 & 1 & -1 & 4 \\ 0 & 1 & -1 & 4 \end(tömb) \jobbra) \begin(tömb) (l) \phantom(0)\\ \phantom(0)\\r_3-r_2\\ r_4-r_2\\r_5+r_2\end(array)\rightarrow\\ $$ $$ \rightarrow\left(\begin(array) (ccc|c) 1 & -1 & 2 & -1\\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \end(tömb) \ jobb) \begin(array) (l) \phantom(0)\\\phantom(0)\\\phantom(0)\\ r_4-r_3\\\phantom(0)\end(array)\rightarrow \left (\begin(tömb) (ccc|c) 1 & -1 & 2 & -1\\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end(tömb) \jobbra) $$

A rendszer kiterjesztett mátrixa lépcsőzetes formára redukálódik. Egy lépésmátrix rangja megegyezik a nem nulla sorok számával, tehát $\rang\widetilde(A)=3$. A $A$ mátrix (a vonalig) szintén lépcsős formává redukálódik, és rangja egyenlő 2, $\rang(A)=2$.

Mivel $\rang A\neq\rang\widetilde(A)$, ezért a Kronecker-Capelli tétel szerint a rendszer inkonzisztens (azaz nincs megoldása).

Válasz: A rendszer inkonzisztens.

3. példa

SLAE felfedezése $ \left\( \begin(aligned) & 2x_1+7x_3-5x_4+11x_5=42;\\ & x_1-2x_2+3x_3+2x_5=17;\\ & -3x_1+9x_2-11x_3-7x_5=-6 ;\\ & -5x_1+17x_2-16x_3-5x_4-4x_5=-90;\\ & 7x_1-17x_2+23x_3+15x_5=132. \end(igazított) \right.$ a kompatibilitás érdekében.

A rendszer kiterjesztett mátrixát lépcsőzetes formába hozzuk:

$$ \left(\begin(array)(ccccc|c) 2 & 0 & 7 & -5 & 11 & 42\\ 1 & -2 & 3 & 0 & 2 & 17 \\ -3 & 9 & -11 & 0 & -7 & -64 \\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \end(array) \right) \overset (r_1\leftrightarrow(r_3))(\rightarrow) $$ $$ \rightarrow\left(\begin(array)(ccccc|c) 1 & -2 & 3 & 0 & 2 & 17\\ 2 & 0 & 7 & -5 & 11 & 42\\ -3 & 9 & -11 & 0 & -7 & -64\\ -5 & 17 & -16 & -5 & -4 & -90 \\ 7 & -17 & 23 & 0 & 15 & 132 \end(tömb) \jobbra) \begin(tömb) (l) \phantom(0)\\ r_2-2r_1 \\r_3+3r_1 \\ r_4+5r_1 \\ r_5-7r_1 \end( tömb) \rightarrow \left(\begin(array)(ccccc|c) 1 & -2 & 3 & 0 & 2 & 17\\ 0 & 4 & 1 & -5 & 7 & 8\\ 0 & 3 & - 2 & 0 & -1 & -13\\ 0 & 7 & -1 & -5 & 6 & -5 \\ 0 & -3 & 2 & 0 & 1 & 13 \end(tömb) \jobbra) \begin( tömb) (l) \phantom(0)\\ \phantom(0)\\4r_3+3r_2 \\ 4r_4-7r_2 \\ 4r_5+3r_2 \end(array) \rightarrow $$ $$ \rightarrow\left(\begin (tömb)(ccccc|c) 1 & -2 & 3 & 0 & 2 & 17\\ 0 & 4 & 1 & -5 & 7 & 8\\ 0 & 0 & -11 & 15 & -25 & -76 \\ 0 & 0 & -11 & 15 & -25 & -76 \\ 0 & 0 & 11 & -15 & 25 & 76 \end(array) \right) \begin(array) (l) \phantom(0 )\\ \phantom(0)\\\phantom(0) \\ r_4-r_3 \\ r_5+r_2 \end(array) \rightarrow \left(\begin(array)(ccccc|c) 1 & -2 & 3 & 0 & 2 & 17\\ 0 & 4 & 1 & -5 & 7 & 8\\ 0 & 0 & -11 & 15 & -25 & -76\\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end(tömb) \jobbra) $$

A rendszer kiterjesztett mátrixát és magának a rendszernek a mátrixát lépcsőzetes formára redukáltuk. A rendszer kiterjesztett mátrixának rangja egyenlő hárommal, a rendszer mátrixának rangja szintén hárommal. Mivel a rendszer $n=5$ ismeretlent tartalmaz, azaz. $\rang\widetilde(A)=\rang(A)\lt(n)$, akkor a Kronecker-Capelli tétel következményének megfelelően ezt a rendszert határozatlan idejű, azaz. végtelen számú megoldása van.

Válasz: a rendszer határozatlan.

A második részben olyan példákat elemezünk, amelyek gyakran szerepelnek a tipikus számításokban ill tesztpapírok felsőbb matematikában: tanulmány az SLAE kompatibilitásával és megoldásával a benne szereplő paraméterek értékétől függően.

Határozza meg, hogy egy lineáris egyenletrendszer konzisztens-e a használatával Kronecker-Capelli tételek gyakran gyorsabban, mint a Gauss-módszer használata, amikor az ismeretlenek szekvenciális kiküszöbölésére van szükség. Ez a tétel egy mátrix rangjának használatán alapul.

A Kronecker-Capelli tétel a rendszerkompatibilitásról. Egy lineáris algebrai egyenletrendszer akkor és csak akkor konzisztens, ha a rendszer mátrixának rangja egyenlő a kiterjesztett mátrix rangjával, azaz.

E mátrixok rangjait az egyenlőtlenség és a mátrix rangja kapcsolja össze BAN BEN csak eggyel több lehet, mint a mátrix rangja A.

Következmény a megoldások számáról szóló Kronecker-Capelli-tételből. Legyen a rendszer m lineáris egyenletek -val n az ismeretlenek teljesítik a kompatibilitási feltételt, vagyis a rendszer együtthatói mátrixának rangja megegyezik a kiterjesztett mátrixának rangjával. Akkor a következő igaz.

Ha egy lineáris egyenletrendszer mátrixának rangja megegyezik az egyenletek számával, vagyis a rendszer konzisztens bármely szabad tagra. Ebben az esetben a kiterjesztett mátrix rangja is m, mivel egy mátrix rangja nem lehet nagyobb, mint a sorok száma.

A Kronecker-Capelli tétel bizonyítása során a rendszer megoldásaira (kompatibilitása esetén) explicit képleteket kaptunk. Ha már ismert, hogy a rendszer konzisztens, akkor a megoldások megtalálásához szükséges:

1) keresse meg a rendszermátrixban A rang nem nulla kisebb rendű, egyenlő a rendszer mátrixának rangjával, vagyis a ranggal r;

2) dobja el azokat az egyenleteket, amelyek megfelelnek a mátrix sorainak A, nem szerepel a mollban ;

3) a jobb oldalon nem szereplő együtthatós kifejezéseket vigye át, majd tetszőleges értékeket adva a jobb oldalon található ismeretleneknek, határozza meg a fennmaradóakat Cramer-képletekkel r ismeretlen a rendszerből r egyenletek nem nulla determinánssal .

1. példa

Megoldás. Kiszámítjuk ennek a rendszernek a mátrixának és a kiterjesztett mátrixnak a rangját. Mindkét esetben egyenlő 3-mal. Ezért a lineáris egyenletrendszer kompatibilis. Mivel a rendszermátrix rangja kisebb, mint az ismeretlenek száma, a rendszernek végtelen sok megoldása van: egy ismeretlen tetszőlegesen felvehető. Kisebb

különbözik a nullától, ezért az utolsó egyenletet elvetjük, és tetszőleges értéket rendelünk az ismeretlenhez.

A fennmaradó ismeretleneket a rendszer határozza meg

Az utolsó rendszert Cramer képleteivel vagy más módon megoldva azt találjuk

Ezt hozzáadva megkapjuk ennek a lineáris egyenletrendszernek az összes megoldását.

2. példa A Kronecker-Capelli tételt követve határozza meg, hogy az egyenletrendszer kompatibilis-e

Ha a rendszer konzisztens, akkor oldja meg.

A gyakorlatban azonban még két eset széles körben elterjedt:

– A rendszer inkonzisztens (nincs megoldása);
A rendszer konzisztens és végtelenül sok megoldást tartalmaz.

jegyzet : a "konzisztencia" kifejezés azt jelenti, hogy a rendszernek van legalább valamilyen megoldása. Számos feladatnál előzetesen meg kell vizsgálni a rendszer kompatibilitását, hogyan kell ezt megtenni - lásd a cikket mátrix rang.

Ezeknél a rendszereknél a leguniverzálisabb megoldási módszereket alkalmazzák - Gauss módszer. Valójában az "iskola" módszer is elvezet a válaszhoz, de a felsőbb matematikában szokás a Gauss-módszert használni az ismeretlenek egymást követő kiküszöbölésére. Aki nem ismeri a Gauss-módszer algoritmust, kérem, először tanulmányozza át a leckét Gauss módszer próbabábukhoz.

Maguk az elemi mátrixtranszformációk pontosan ugyanazok, a különbség a megoldás végén lesz. Először nézzünk meg néhány olyan példát, ahol a rendszernek nincs megoldása (inkonzisztens).

1. példa

Mi az, ami azonnal megakad ebben a rendszerben? Az egyenletek száma kevesebb, mint a változók száma. Ha az egyenletek száma kisebb, mint a változók száma, akkor azonnal kijelenthetjük, hogy a rendszer vagy inkonzisztens, vagy végtelen sok megoldása van. És már csak ki kell deríteni.

A megoldás eleje teljesen hétköznapi - felírjuk a rendszer kiterjesztett mátrixát, és elemi transzformációkkal lépésenkénti formába hozzuk:

(1) A bal felső lépésben +1-et vagy -1-et kell kapnunk. Az első oszlopban nincsenek ilyen számok, így a sorok átrendezése nem fog működni. Az egységet önállóan kell megszervezni, és ez többféleképpen is megtehető. Ezt tettem: Az első sorhoz adja hozzá a harmadik sort, megszorozva -1-gyel.

(2) Most két nullát kapunk az első oszlopban. A második sorhoz hozzáadjuk az első sort 3-mal szorozva. A harmadik sorhoz hozzáadjuk az első sort 5-tel szorozva.

(3) Az átalakítás után mindig célszerű megnézni, hogy lehetséges-e egyszerűsíteni a kapott karakterláncokat? Tud. A második sort elosztjuk 2-vel, ugyanakkor a második lépésben megkapjuk a kívánt -1-et. Osszuk el a harmadik sort -3-mal.

(4) Adja hozzá a második sort a harmadikhoz.

Valószínűleg mindenki felfigyelt a rossz vonalra, amely az elemi átalakítások eredményeként alakult ki: . Nyilvánvaló, hogy ez nem lehet így. Valójában átírjuk a kapott mátrixot vissza a lineáris egyenletrendszerhez:

Ha az elemi transzformációk eredményeként olyan alakú karakterláncot kapunk, ahol nem nulla szám, akkor a rendszer inkonzisztens (nincs megoldása) .

Hogyan rögzítsük egy feladat végét? Rajzoljuk le fehér krétával: "elemi átalakítások eredményeképpen egy alaksort kapunk, ahol" és adjuk meg a választ: a rendszernek nincsenek megoldásai (inkonzisztens).

Ha a feltételnek megfelelően a rendszer kompatibilitásának FELFEDEZÉSE szükséges, akkor a koncepciót magában foglaló, szolidabb stílusú megoldást kell kiadni. mátrix rang és a Kronecker-Capelli tétel.

Kérjük, vegye figyelembe, hogy itt nincs a Gauss-algoritmus fordított mozgása - nincsenek megoldások, és egyszerűen nincs mit találni.

2. példa

Oldjon meg egy lineáris egyenletrendszert!

Ez egy „csináld magad” példa. Teljes megoldás és válasz a lecke végén. Ismételten emlékeztetlek arra, hogy az Ön megoldási útvonala eltérhet az én megoldási útvonalamtól, a Gauss-algoritmusnak nincs erős „merevsége”.

Még egy technikai jellemzője a megoldásnak: az elemi transzformációk leállíthatók Egyszerre, amint egy olyan sort, mint , hol . Vegyünk egy feltételes példát: tegyük fel, hogy az első transzformáció után kapunk egy mátrixot . A mátrix még nem redukálódott lépcsős formára, de nincs szükség további elemi transzformációkra, hiszen megjelent a formának egy sora, ahol . Azonnal azt kell válaszolni, hogy a rendszer nem kompatibilis.

Ha egy lineáris egyenletrendszernek nincs megoldása, az szinte ajándék, mert rövid megoldást kapunk, néha szó szerint 2-3 lépésben.

De ezen a világon minden kiegyensúlyozott, és a probléma, amelyre a rendszernek végtelenül sok megoldása van, csak hosszabb.

3. példa

Oldjon meg egy lineáris egyenletrendszert!

4 egyenlet és 4 ismeretlen, tehát a rendszernek vagy egyetlen megoldása lehet, vagy nincs megoldása, vagy végtelen sok megoldása lehet. Bármi is volt, de a Gauss-módszer mindenképpen elvezet minket a válaszhoz. Ebben rejlik a sokoldalúsága.

Az eleje ismét szabványos. Felírjuk a rendszer kiterjesztett mátrixát, és elemi transzformációkkal lépésformára hozzuk:

Ez minden, és féltél.

(1) Vegye figyelembe, hogy az első oszlopban lévő összes szám osztható 2-vel, így a 2 megfelelő a bal felső létrafokon. A második sorhoz hozzáadjuk az első sort, megszorozva -4-gyel. A harmadik sorhoz hozzáadjuk az első sort, megszorozva -2-vel. A negyedik sorhoz hozzáadjuk az első sort, megszorozva -1-gyel.

Figyelem! Sokan kísértésbe eshetnek a negyedik sorból kivonni első sor. Ezt meg lehet tenni, de nem szükséges, a tapasztalat azt mutatja, hogy a számítási hiba valószínűsége többszörösére nő. Csak add össze: a negyedik sorhoz add hozzá az első sort, megszorozva -1-gyel - pontosan!

(2) Az utolsó három sor arányos, ebből kettő törölhető.

Itt ismét meg kell mutatni fokozott figyelem, de tényleg arányosak a vonalak? Viszontbiztosításnál (különösen teáskannánál) nem lenne felesleges a második sort -1-gyel megszorozni, a negyedik sort pedig 2-vel osztani, így három egyforma sort kapunk. És csak ezután távolítson el kettőt.

Az elemi átalakítások eredményeként a rendszer kiterjesztett mátrixa lépcsőzetes formára redukálódik:

A feladat füzetben való elkészítésekor az áttekinthetőség kedvéért célszerű ugyanezeket a jegyzeteket ceruzával elkészíteni.

Átírjuk a megfelelő egyenletrendszert:

A rendszer „szokásos” egyetlen megoldásának itt nincs szaga. Nincs rossz sor sem. Ez azt jelenti, hogy ez a harmadik fennmaradó eset – a rendszernek végtelen sok megoldása van. Néha, feltételek szerint, szükséges a rendszer kompatibilitásának vizsgálata (vagyis annak bizonyítása, hogy egyáltalán létezik megoldás), erről a cikk utolsó bekezdésében olvashat. Hogyan találjuk meg a mátrix rangját? De most bontsuk le az alapokat:

A rendszer végtelen megoldáshalmazát röviden az ún általános rendszermegoldás .

A rendszer általános megoldását a Gauss-módszer fordított mozgásával fogjuk megtalálni.

Először is meg kell határoznunk, hogy milyen változóink vannak alapvető, és mely változók ingyenes. Nem kell bajlódni a lineáris algebra feltételeivel, elég megjegyezni, hogy vannak ilyenek bázisváltozókÉs szabad változók.

Az alapváltozók mindig szigorúan a mátrix lépésein „ülnek”..
Ebben a példában az alapváltozók és

A szabad változók minden többi változók, amelyek nem kaptak lépést. A mi esetünkben ezek közül kettő van: – szabad változók.

Most kell Minden bázisváltozók Expressz csak keresztül szabad változók.

A Gauss-algoritmus fordított mozgása hagyományosan alulról felfelé működik.
A rendszer második egyenletéből az alapváltozót fejezzük ki:

Most nézzük meg az első egyenletet: . Először behelyettesítjük a talált kifejezést:

Az alapváltozót szabad változókkal kell kifejezni:

Az eredmény az, amire szüksége van - Minden az alapváltozók ( és ) vannak kifejezve csak keresztül szabad változók:

Valójában az általános megoldás készen áll:

Hogyan írjuk le az általános megoldást?
A szabad változók "önmagukban" és szigorúan a helyükre kerülnek az általános megoldásba. Ebben az esetben a szabad változókat a második és a negyedik pozícióba kell írni:
.

Az eredményül kapott kifejezések az alapváltozókhoz és nyilvánvalóan az első és a harmadik pozícióba kell írni:

Szabad változók megadása tetszőleges értékek, végtelenül sok van privát döntések. a legtöbben népszerű értékek nullák, mivel az adott megoldás a legkönnyebben elérhető. Csere az általános megoldásban:

ez magándöntés.

Az egyik egy másik édes pár, cseréljük be az általános megoldásba:

egy másik speciális megoldás.

Könnyen belátható, hogy az egyenletrendszer rendelkezik végtelenül sok megoldás(mivel szabad változókat adhatunk Bármiértékek)

Minden egyes egy adott megoldásnak meg kell felelnie mindenkinek rendszeregyenlet. Ez az alapja a megoldás helyességének „gyors” ellenőrzésének. Vegyünk például egy adott megoldást, és cseréljük be az eredeti rendszer minden egyenletének bal oldalára:

Mindennek össze kell jönnie. És minden adott megoldásnál mindennek konvergálnia kell.

De szigorúan véve egy adott megoldás ellenőrzése néha csal; egy adott megoldás kielégítheti a rendszer minden egyenletét, és magát az általános megoldást valójában helytelenül találjuk meg.

Ezért az általános megoldás ellenőrzése alaposabb és megbízhatóbb. Hogyan ellenőrizhető a kapott általános megoldás ?

Könnyű, de elég fárasztó. Kifejezéseket kell vennünk alapvető változók, ebben az esetben és , és cserélje be őket a rendszer minden egyenletének bal oldalára.

A rendszer első egyenletének bal oldalán:

A rendszer második egyenletének bal oldalán:

Az eredeti egyenlet jobb oldalát kapjuk.

4. példa

Oldja meg a rendszert Gauss módszerrel! Keressen egy általános és két privát megoldást. Ellenőrizze az általános megoldást.

Ez egy „csináld magad” példa. Itt egyébként megint kevesebb az egyenletek száma, mint az ismeretleneké, ami azt jelenti, hogy azonnal világos, hogy a rendszer vagy inkonzisztens lesz, vagy végtelen számú megoldással. Mi a fontos magában a döntési folyamatban? Figyelem, és még egyszer figyelem. Teljes megoldás és válasz a lecke végén.

És még néhány példa az anyag megerősítésére

5. példa

Oldjon meg egy lineáris egyenletrendszert! Ha a rendszernek végtelen sok megoldása van, keressen két konkrét megoldást, és ellenőrizze az általános megoldást

Megoldás: Írjuk fel a rendszer kiterjesztett mátrixát és elemi transzformációk segítségével hozzuk lépésformába:

(1) Adja hozzá az első sort a másodikhoz. A harmadik sorhoz hozzáadjuk az első sort 2-vel szorozva. A negyedik sorhoz hozzáadjuk az első sort 3-mal szorozva.
(2) A harmadik sorhoz adja hozzá a második sort, megszorozva -5-tel. A negyedik sorhoz hozzáadjuk a második sort, megszorozva -7-tel.
(3) A harmadik és a negyedik sor megegyezik, az egyiket töröljük.

Íme egy ilyen szépség:

Az alapváltozók lépcsőkön helyezkednek el, tehát alapváltozók.
Csak egy szabad változó van, amely nem kapott lépést:

Fordított mozgás:
Az alapváltozókat a szabad változóval fejezzük ki:
A harmadik egyenletből:

Tekintsük a második egyenletet, és cseréljük be a talált kifejezést:

Tekintsük az első egyenletet, és helyettesítsük be a talált kifejezéseket és ebbe:

Igen, a közönséges törteket számoló számológép továbbra is kényelmes.

Tehát az általános megoldás:

Még egyszer, hogyan történt? A szabad változó egyedül a jogos negyedik helyen áll. Az alapváltozók eredményül kapott kifejezései szintén elfoglalták sorszámukat.

Azonnal ellenőrizzük az általános megoldást. Dolgozz a feketéknek, de már megcsináltam, szóval fogd =)

A rendszer minden egyenletének bal oldalába behelyettesítünk három hőst , :

Az egyenletek megfelelő jobb oldalait megkapjuk, így az általános megoldás helyesen található.

Most a megtalált általános megoldásból két konkrét megoldást kapunk. A séf itt az egyetlen szabad változó. Nem kell törni a fejét.

Akkor hagyd ez magándöntés.
Akkor hagyd egy másik speciális megoldás.

Válasz: Közös döntés: , speciális megoldások: , .

Hiába emlékeztem itt a feketékre ... ... mert mindenféle szadista motívumok jártak a fejemben és eszembe jutott a jól ismert fotozhaba, amiben a Ku Klux Klansmen fehér overálban fut át a pályán egy fekete focista után. . Ülök és csendesen mosolygok. Tudod milyen zavaró…

A sok matematika káros, ezért egy hasonló végső példa egy független megoldáshoz.

6. példa

Keresse meg a lineáris egyenletrendszer általános megoldását!

Az általános megoldást már megnéztem, a válaszban meg lehet bízni. Az Ön megoldása eltérhet az én megoldásomtól, a lényeg, hogy az általános megoldások egyezzenek.

Valószínűleg sokan észrevettek egy kellemetlen pillanatot a megoldásokban: nagyon gyakran a Gauss-módszer fordított lefolyása során kellett a közönséges törtekkel babrálni. A gyakorlatban ez igaz, sokkal ritkábban fordulnak elő olyan esetek, amikor nincs tört. Legyen felkészült lelkileg, és ami a legfontosabb, technikailag.

Kitérek a megoldás néhány olyan jellemzőjére, amelyek nem szerepeltek a megoldott példákban.

A rendszer általános megoldása néha tartalmazhat konstanst (vagy állandókat), például: . Itt az egyik alapváltozó egy állandó számmal egyenlő: . Ebben nincs semmi egzotikus, előfordul. Nyilvánvaló, hogy ebben az esetben minden konkrét megoldás ötöst tartalmaz az első helyen.

Ritkán, de vannak olyan rendszerek, amelyekben az egyenletek száma nagyobb, mint a változók száma. A Gauss-módszer a legsúlyosabb körülmények között is működik, nyugodtan kell a rendszer kiterjesztett mátrixát lépcsőzetes formába hozni a szabványos algoritmus szerint. Lehet, hogy egy ilyen rendszer inkonzisztens, végtelenül sok megoldást tartalmazhat, és furcsa módon egyedi megoldása is lehet.