Egy fok tulajdonságainak megismétlése természetes kitevővel. A „természetes mutatóval végzett fokozat” óra fejlesztése. VI Egészségvédő technológiák elemei (13. dia)
Előnézet:
ÖNKORMÁNYZATI KÖLTSÉGVETÉSI ÁLTALÁNOS OKTATÁSI INTÉZMÉNY
11. számú KÖZÉPISKOLA
ÖNKORMÁNYZAT VÁROS - ANAPA ÜDÜLŐDÉS
„Fizikai és matematikai tudományok (matematika)” jelölés
Terv - óra összefoglaló a témában:
7. osztály
Kidolgozó: Bykova E.A., a legmagasabb képesítési kategóriájú matematikatanár
Anapa, 2013
Nyílt óra algebra 7. osztályban a következő témában:
"Fokozat tulajdonságai természetes kitevővel"
Az óra céljai:
Nevelési:- a fokozattal kapcsolatos ismeretek naturális jelzővel történő rendszerezésére, általánosítására, a fokozatokat tartalmazó kifejezések természetes jelzővel történő legegyszerűbb átalakítási készségeinek megszilárdítására, fejlesztésére.
Nevelési: - nevelés kognitív tevékenység, felelősségérzet, kommunikációs kultúra, párbeszéd kultúrája.
Fejlesztés: - a vizuális memória, a matematikailag művelt beszéd, a logikus gondolkodás fejlesztése, az oktatási anyagok tudatos észlelése.
Feladatok:
1. Tárgy: ismételje meg, általánosítsa és rendszerezze a témával kapcsolatos ismereteket, teremtsen feltételeket a tudás és készségek asszimilációjának ellenőrzéséhez (kölcsönös ellenőrzéséhez); folytassa a hallgatók motivációjának kialakítását a tantárgy tanulására.
2. Metatárgy: operatív gondolkodási stílus kialakítása, a tanulók közös munka során a kommunikációs készségek elsajátításának elősegítése, kreatív gondolkodásuk aktivizálása; a tanulók olyan kompetenciáinak kialakításának folytatása, amelyek hozzájárulnak hatékony szocializációjukhoz, önképzési és önképzési készségeikhez
3. Személyes: kultúra nevelése, a személyes tulajdonságok kialakulásának elősegítése, amelyek célja az emberekhez, az élethez való jóindulatú, toleráns hozzáállás; a tevékenységekben a kezdeményezés és a függetlenség ápolása; annak megértéséhez, hogy a vizsgált témára van szükség az állami záróbizonyítványra való sikeres felkészüléshez.
Az óra típusa: általános lecke a témában.
Az óra típusa: kombinált.
Az óra felépítése:
1. Szervezeti mozzanat.
2. Az óra témájának, céljainak és célkitűzéseinek közlése.
3. A tanultak reprodukálása és alkalmazása standard helyzetekben.
4. A megszerzett ismeretek átadása, elsődleges alkalmazása új vagy megváltozott körülmények között, a készségek kialakítása érdekében.
5. Egészségmegőrző technológiák elemei.
6. Tanulói feladatok önálló elvégzése tanári felügyelet mellett.
7. Az óra összegzése és a házi feladat felállítása.
Felszerelés: multimédiás projektor, számítógép.
Bemutató a Microsoft Office Power Point 2007-ben(1. melléklet)
Tanterv:
Lecke szakasz | Idő |
||
Idő szervezése. | Rendeljen tanulókat a leckéhez | 1 perc. |
|
Házi feladat ellenőrzése | Hibajavítás | 3 perc |
|
Az óra üzenettémái, céljai és célkitűzései. | Az órai célok kitűzése | 1 perc. |
|
szóbeli munka. Egy fok tulajdonságainak megismétlése természetes kitevővel. | Frissítse az alapvető ismereteket | 7 perc. |
|
Edző gyakorlatok. | A fokszám-átváltás készségének formálása természetes jelzővel. | 10 perc. |
|
Fizikai szünet. | Egészségmegőrző technológiák alkalmazása | 2 perc. |
|
Egyedi Ellenőrző munka kártyákkal. | Hibajavítás | 12 perc |
|
Az óra eredményei. | Foglalja össze a leckében szerzett elméleti információkat! | 2 perc |
|
Házi feladat beállítása. | Ismertesse a házi feladat tartalmát! | 2 perc |
Irodalom:
1. Algebra: tankönyv. 7 cellához. Általános oktatás intézmények / Yu.N. Makarychev, N. G. Mindyuk és mások; szerkesztette: S.A. Teljakovszkij. – M.: Felvilágosodás, 2008.
2. Zvavich L.I., Kuznetsova L.V., Suvorova S.B. Didaktikai anyagok algebráról a 7. osztályhoz. – M.: Felvilágosodás, 2009.
3. Tesztfeladatok gyűjtése tematikus és végső ellenőrzéshez. Algebra 7. évfolyam./ S.A. Puskin, I. L. Guszev. - M .: "Intellektus", 2013.
4. T.Yu.Dyumina, A.A. Makhonina, „Algebra. Óratervek." - Volgograd: "Tanár", 2013
Az órák alatt
1. Szervezeti mozzanat.
2. Házi feladat ellenőrzése
3. Az óra témája. Az óra céljai és célkitűzései.
Matematika, barátok,
Abszolút mindenkinek szüksége van rá.
Dolgozz keményen az órán
És siker vár rád!
4. Szóbeli munka.
a) Fokozat tulajdonságainak megismétlése természetes jelzővel. Adott egy asztal. A bal oldali oszlopban töltse ki a hiányzó helyeket, a jobb oldalon - végezze el a feladatokat.
A mértéke a természetes indikátorral P ____________ P ____________, amelyek mindegyike az A. | 1. Adja meg a terméket fokozatként: A). (-8) * (-8) * (-8) * (-8) * (-8) * ; b). (x-y) * (x-y) * (x-y) * (x-y) * ; 2. Emelje hatványra: 3 4 ; (-0,2) 3 ; (2/3) 2 Nevezze meg az alapot és a kitevőt felírva! |
Ha a hatványokat ugyanazzal az alappal szorozzuk meg, a ________________________-t adjuk hozzá. | Kovesd ezeket a lepeseket: a 4 * a 12; a 6 * a 9 * a; 3 2 * 3 3 |
Ha azonos bázisú hatványokat osztunk fel, a ___________ változatlan marad, a __________ számlálóból pedig a _____________ __________ nevezőt. | Kovesd ezeket a lepeseket: a 12: a 4; n 9 : n 3 : n ; 3 5 : 3 2 |
Ha egy hatványt hatványra emelünk, _______________ változatlan marad, és __________ megszorozzuk. | Kovesd ezeket a lepeseket:
(m 3 ) 7; (k 4 ) 5; (4 2 ) 3 |
Hatványra emeléskor a szorzatokat erre a hatványra emeljük ________________ ____________, és az eredményeket megszorozzuk. | Hatványozás végrehajtása: (-2 a 3 b 2) 5; (1/3p 2 q 3 ) 3 |
Ereje a , nem egyenlő nullával, nulla kitevővel egyenlő | Kiszámítja: 3x 0 x= 2,6-nál |
b) A fokozatokat tartalmazó kifejezések transzformációjával kapcsolatos feladatok elvégzése során a hallgató a következő hibákat követte el:(írás a táblára)
1) a) ; b)
;
V) ; G)
;
2) a) ; b)
;
V) ; G)
;
3) a) ; b)
;
V) .
Milyen definíciókat, tulajdonságokat, szabályokat nem tud a tanuló?
5. Edző gyakorlatok.
447. sz. - a táblán és a füzetekben részletes megjegyzésekkel, a fokozatok tulajdonságainak felhasználásával;
450. sz. (a, c) - a táblán és a füzetekben;
445. szám - szóban.
6. Fizikai perc
Gyorsan felkelt, mosolygott,
Feljebb húzva.
Nos, egyenesítse ki a vállát
Emelje fel, engedje le.
Forduljon jobbra, forduljon balra
Érintse meg a kezét a térdével.
Ülj le, kelj fel, ülj le, kelj fel
És a helyszínen futottak.
Az ifjúság veled tanul
Fejleszd az akaratot és a találékonyságot egyaránt.
7. Egyéni próbamunka.
Minden tanuló elvégzi a feladatokat, hozzájuk tartozik egy kulcs, amelyben a teljes ábécé a válaszok betűk szerinti tippelésének kizárására szolgál. Jó döntés esetén - a megfelelő szó.
Az egyes sorok feladatai egyediek.
sz. p / p | Feladat 1 sor | sz. p / p | 2. feladatsor | sz. p / p | 3. feladatsor |
m 3 * m 2 * m 8 | a 4 * a 3 * a 2 | a 4 * a * a 3 * a |
|||
p20 : p17 | (2 4 ) 5 : (2 7 ) 2 | (7x)2 |
|||
c 5 : c 0 | 3 * 3 2 * 3 0 | p*p2*p0 |
|||
(3a) 3 | (2y)5 | c * c 3 * c |
|||
m * m 5 * m 3 * m 0 | (m 2 ) 4 * m | m * m 4 * (m 2 ) 2 * m 0 |
|||
2 14 : 2 8 | (2 3 ) 2 | (2 3 ) 7 : (2 5 ) 3 |
|||
(-x) 3*x4 | (-x 3 ) *(- x) 4 | X 3 * (-x) 4 |
|||
(p * p 3) : 5. o | (p 2 * p 5 ): p 4 * p 0 | (p 2 ) 4 : p 5 |
|||
3 7 * (3 2 ) 3 : 3 10 | (3 5 ) 2 * 3 7 : 3 14 | (3 4 ) 2 * (3 2 ) 3 : 3 11 |
Kulcs
32y5 | 49x2 | 27a 3 |
|||||||
m 13 | |||||||||
81a 3 | 16a4 | 10y5 | 9y7 | 32x5 | 49y3 |
||||
A munka eredményeit egy dián jelenítjük meg önvizsgálat céljából:
Matematika
8. Óra összefoglalója:
Óra összegzése, osztályozás.
- Sorolja fel a fok tulajdonságait természetes kitevővel!
Az óra osztályzatait a munka tesztekkel történő ellenőrzése után állítják fel, figyelembe véve azon tanulók válaszait, akik az órán válaszoltak.
Találd ki a keresztrejtvényt
Függőlegesen:
- Ő oszt
- Elemi figura a repülőn
- Valódi egyenlőség
- Egy kilenc nullával
- Egy hasonlóval van egymásra rakva
- Kettő a három erejéig
Vízszintesen:
2. Egy háromszög oldalainak száma
4. Monomok összege
5. Foglalja össze
7. Egy kör egy pontját a középpontjával összekötő szakasz
8. Van egy számlálója és egy nevezője
9. Házi feladat:
Az n természetes kitevővel rendelkező a szám fokszámát ________________ n ____________-nak nevezzük, amelyek mindegyike egyenlő a-val. 1. Adja meg a szorzatot fokban: a). (-8) * (-8) * (-8) * (-8) * (-8) * ; b). (x-y)* (x-y) * (x-y) * (x-y) * ; 2. Hatványra emelés: 3 4 ; (-0,2) 3; (2 /3) 2 Nevezze meg az írott hatványok alapját és kitevőjét! Ha a hatványokat ugyanazzal az alappal szorozzuk meg, a ________________________-t adjuk hozzá. Tegye a következőket: a 4 * a 12; a 6 * a 9 * a; 3 2 * 3 3 Ha a fokokat azonos alapokkal osztjuk fel, ___________ változatlan marad, a __________ számlálóból pedig _____________ __________ nevezőt. Kövesse az alábbi lépéseket: a 12: a 4; p 9: p 3: p; 3 5: 3 2 Ha egy hatványt hatványra emelünk, _______________ változatlan marad, és __________ megszorozzuk. Kovesd ezeket a lepeseket: ; (m 3) 7; (k 4) 5; (4 2) 3 Hatványra emeléskor a szorzatokat erre a hatványra emeljük _________________ ____________, és az eredményeket megszorozzuk. Hatványozás végrehajtása: (-2 a 3 b 2) 5 ; (1 /3p 2 q 3) 3 Nem nulla a hatványa kitevővel egyenlő. Számítsa ki: 3 x 0 x = 2,6 Ismételje meg!
Ötletelés
Gyorsan felálltak, mosolyogtak, egyre feljebb húzták magukat. Nos, egyenesítsd ki a vállad, emeld fel, engedd le. Fordulj jobbra, fordulj balra, Érintsd meg a kezed a térddel. Leültek, felkeltek, leültek, felkeltek, És a helyszínen futottak. A fiatalság veled tanul Az akarat és a találékonyság fejlesztése.
Egyéni próbamunka p / p sz. feladat 1. sor p / p. feladat 2. sor p / p 3. sor 1 m 3 * m 2 * m 8 1 a 4 * a 3 * a 2 1 a 4 * a * a 3 * a 2 p 20: p 17 2 (2 4) 5: (2 7) 2 2 (7x) 2 3 c 5: c 0 3 3 * 3 2 * 3 0 3 p * p 2 * p 0 4 (3a ) 3 4 (2 év) 5 4 c * c 3 * c 5 m * m 5 * m 3 * m 0 5 (m 2) 4 * m 5 m * m 4 * (m 2) 2 * m 0 6 2 14 : 2 8 6 (2 3) 2 6 (2 3) 7: (2 5) 3 7 (-x) 3 * x 4 7 (-x 3) * (- x) 4 7 -x 3 * (-x ) 4 8 (p * p 3) : p 5 8 (p 2 * p 5) : p 4 * p 0 8 (p 2) 4: p 5 9 3 7 * (3 2) 3: 3 10 9 (3 5) 2*3 7:3 14 9 (3 4) 2* (3 2) 3:3 11
Ellenőrizd le magadat! Kulcs! A B C D E F G I J m 9 32y 5 81 a 9 x 3 49x 2 m 5 p 4 c 5 27a 3 L M O P R S T U V 64 3 4 p 3 27 2 5 x 7 p 6 m 3 m 13 a 8 X C W W 7 81as 10 év 5 9 év 7 -x 7 a 2 32x 5 49 év 3 I x 5
matematika
KITALÁLJA A KERESZTSZÓT Függőlegesen: 1. Osztja az osztalékot 2. Egy elemi alak a síkon 3. Valódi egyenlőség 4. Egy kilenc nullával 5. Hozzáadjuk a hasonlóhoz 6. Kettőt a három hatványához Vízszintesen: 2. A a háromszög oldalainak száma 4. A monomok összege 5. Összegzés 7. Egy kör egy pontját a középpontjával összekötő szakasz 8. Van egy számlálója és egy nevezője
Óraösszefoglaló Osztályozás Feladat házi feladat Válaszolj a kérdésekre 101. o., 450. (b, d), 534., 453. sz.
Korábban már beszéltünk arról, hogy mi a szám hatványa. Vannak bizonyos tulajdonságai, amelyek hasznosak a problémák megoldásában: ezeket és az összes lehetséges kitevőt elemezzük ebben a cikkben. Példákkal is bemutatjuk, hogyan lehet ezeket a gyakorlatban bizonyítani és helyesen alkalmazni.
Emlékezzünk vissza a természetes kitevővel rendelkező fok fogalmára, amelyet már korábban megfogalmaztunk: ez az n-edik számú tényező szorzata, amelyek mindegyike egyenlő a-val. Emlékeznünk kell arra is, hogyan kell helyesen szorozni a valós számokat. Mindez segít abban, hogy egy természetes mutatóval a következő tulajdonságokat fogalmazzuk meg egy diplomához:
1. definíció
1. A fok fő tulajdonsága: a m a n = a m + n
Általánosítható: a n 1 · a n 2 · … · a n k = a n 1 + n 2 + … + n k.
2. Azonos bázisú hatványok hányados tulajdonsága: a m: a n = a m − n
3. Termékfok tulajdonság: (a b) n = a n b n
Az egyenlőség kiterjeszthető a következőkre: (a 1 a 2 … a k) n = a 1 n a 2 n … a k n
4. Természetes fok tulajdonsága: (a: b) n = a n: b n
5. A hatványt a következő hatványra emeljük: (a m) n = a m n ,
Általánosítható: (((a n 1) n 2) …) n k = a n 1 n 2 … n k
6. Hasonlítsa össze a fokot nullával:
- ha a > 0, akkor bármely természetes n esetén a n nagyobb lesz nullánál;
- ha a egyenlő 0, akkor a n is egyenlő lesz nullával;
- a< 0 и таком показателе степени, который будет четным числом 2 · m , a 2 · m будет больше нуля;
- a< 0 и таком показателе степени, который будет нечетным числом 2 · m − 1 , a 2 · m − 1 будет меньше нуля.
7. Egyenlőség a n< b n будет справедливо для любого натурального n при условии, что a и b больше нуля и не равны друг другу.
8. Az a m > a n egyenlőtlenség akkor lesz igaz, ha m és n természetes számok, m nagyobb n-nél és a nagyobb nullánál és nem kisebb egynél.
Ennek eredményeként több egyenlőséget kaptunk; ha az összes fent jelzett feltételnek megfelel, akkor azok azonosak lesznek. Mindegyik egyenlőségnél, például a főtulajdonságnál, felcserélheti a jobb és bal részt: a m · a n = a m + n - ugyanaz, mint a m + n = a m · a n . Ebben a formában gyakran használják kifejezések egyszerűsítésére.
1. Kezdjük a fok fő tulajdonságával: az a m · a n = a m + n egyenlőség igaz lesz bármely természetes m és n és valós a esetén. Hogyan lehet ezt az állítást bizonyítani?
A természetes kitevőkkel rendelkező hatványok alapvető meghatározása lehetővé teszi számunkra, hogy az egyenlőséget tényezők szorzatává alakítsuk. Ilyen bejegyzést fogunk kapni:
Ezt le lehet rövidíteni ![]() (idézzük fel a szorzás alapvető tulajdonságait). Ennek eredményeként megkaptuk az a szám fokszámát m + n természetes kitevővel. Így a m + n, ami azt jelenti, hogy a fok fő tulajdonsága bizonyítva van.
(idézzük fel a szorzás alapvető tulajdonságait). Ennek eredményeként megkaptuk az a szám fokszámát m + n természetes kitevővel. Így a m + n, ami azt jelenti, hogy a fok fő tulajdonsága bizonyítva van.
Elemezzük konkrét példa ezt megerősítve.
1. példa
Tehát két hatványunk van a 2-es bázissal. Természetes mutatójuk 2, illetve 3. Megkaptuk az egyenlőséget: 2 2 2 3 = 2 2 + 3 = 2 5 Számítsuk ki az értékeket, hogy ellenőrizzük ennek az egyenlőségnek a helyességét.
Végezzük el a szükséges matematikai műveleteket: 2 2 2 3 = (2 2) (2 2 2) = 4 8 = 32 és 2 5 = 2 2 2 2 2 = 32
Ennek eredményeként a következőt kaptuk: 2 2 2 3 = 2 5 . Az ingatlan bizonyított.
A szorzás tulajdonságaiból adódóan a tulajdonságot általánosíthatjuk úgy, hogy három vagy több hatvány formájában fogalmazzuk meg, amelyeknél a kitevők természetes számok, az alapok pedig azonosak. Ha k betűvel jelöljük az n 1, n 2 stb. természetes számok számát, akkor a helyes egyenlőséget kapjuk:
a n 1 a n 2 … a n k = a n 1 + n 2 + … + n k.
2. példa
2. Ezután be kell bizonyítanunk a következő tulajdonságot, amelyet hányados tulajdonságnak nevezünk, és amely az azonos alapú hatványokban rejlik: ez az a m egyenlőség: a n = a m − n , amely bármely természetes m-re és n-re (és m-re) érvényes. nagyobb, mint n)) és bármely nem nulla valós a .
Először is magyarázzuk el, hogy pontosan mit is jelentenek a megfogalmazásban említett feltételek. Ha nullával egyenlőt veszünk, akkor a végén nullával való osztást kapunk, ami nem tehető meg (végül is 0 n = 0). Az a feltétel, hogy az m számnak nagyobbnak kell lennie n-nél, szükséges ahhoz, hogy a természetes kitevőn belül maradhassunk: m-ből n-t kivonva természetes számot kapunk. Ha a feltétel nem teljesül, negatív számot vagy nullát kapunk, és ismét túllépünk a fokok természetes mutatókkal való vizsgálatán.
Most rátérhetünk a bizonyításra. A korábban vizsgáltakból felidézzük a törtek alapvető tulajdonságait, és a következőképpen fogalmazzuk meg az egyenlőséget:
a m − n a n = a (m − n) + n = a m
Ebből következtethetünk: a m − n a n = a m
Emlékezzünk az osztás és szorzás közötti összefüggésre. Ebből következik, hogy a m − n az a m és a n hatványok hányadosa. Ez a másodfokú tulajdonság bizonyítéka.
3. példa
Helyettesítsen számokat a mutatók egyértelműsége érdekében, és jelölje a π fokszám alapját: π 5: π 2 = π 5 − 3 = π 3
3. Ezután elemezzük a szorzat fokának tulajdonságát: (a · b) n = a n · b n bármely valós a és b és természetes n esetén.
A természetes kitevős fokozat alapdefiníciója szerint az egyenlőséget a következőképpen fogalmazhatjuk meg újra:

Emlékezve a szorzás tulajdonságaira, írjuk:  . Ugyanazt jelenti, mint a n · b n.
. Ugyanazt jelenti, mint a n · b n.
4. példa
2 3 - 4 2 5 4 = 2 3 4 - 4 2 5 4
Ha három vagy több tényezőnk van, akkor ez a tulajdonság erre az esetre is vonatkozik. Bevezetjük a faktorszám k jelölését, és felírjuk:
(a 1 a 2 … a k) n = a 1 n a 2 n … a k n
5. példa
Adott számokkal a következő helyes egyenlőséget kapjuk: (2 (- 2 , 3) a) 7 = 2 7 (- 2 , 3) 7 a
4. Ezek után megpróbáljuk igazolni a hányados tulajdonságot: (a: b) n = a n: b n bármely valós a és b esetén, ha b nem egyenlő 0-val és n természetes szám.
A bizonyításhoz használhatjuk az előző fokozat tulajdonságot. Ha (a: b) n b n = ((a: b) b) n = a n, és (a: b) n b n = a n, akkor ebből az következik, hogy (a: b) n a n b n-nel való osztásának hányadosa.
6. példa
Számoljuk a példát: 3 1 2: - 0 . 5 3 = 3 1 2 3: (- 0 , 5) 3
7. példa
Kezdjük rögtön egy példával: (5 2) 3 = 5 2 3 = 5 6
És most megfogalmazunk egy egyenlőségláncot, amely bebizonyítja számunkra az egyenlőség helyességét: 
Ha a példában vannak fokszámaink, akkor ez a tulajdonság rájuk is igaz. Ha vannak p, q, r, s természetes számok, akkor igaz lesz:
a p q y s = a p q y s
8. példa
Adjunk hozzá konkrétumokat: (((5 , 2) 3) 2) 5 = (5 , 2) 3 2 5 = (5 , 2) 30
6. A természetes kitevővel rendelkező fokok másik tulajdonsága, amelyet bizonyítanunk kell, az összehasonlítási tulajdonság.
Először is hasonlítsuk össze a kitevőt nullával. Miért a n > 0, feltéve, hogy a nagyobb, mint 0?
Ha egy pozitív számot megszorozunk egy másikkal, akkor pozitív számot is kapunk. Ennek a ténynek a ismeretében azt mondhatjuk, hogy ez nem függ a tényezők számától - tetszőleges számú pozitív szám szorzásának eredménye pozitív szám. És mi a fok, ha nem a számok szorzásának eredménye? Akkor ez minden pozitív bázisú és természetes kitevővel rendelkező n hatványra igaz lesz.
9. példa
3 5 > 0 , (0 , 00201) 2 > 0 és 34 9 13 51 > 0
Az is nyilvánvaló, hogy a nullával egyenlő bázisú hatvány maga is nulla. Bármilyen teljesítményre nullát emelünk, az nulla marad.
10. példa
0 3 = 0 és 0 762 = 0
Ha a fokszám alapja egy negatív szám, akkor a bizonyítás egy kicsit bonyolultabb, mivel a páros / páratlan kitevő fogalma válik fontossá. Kezdjük azzal az esettel, amikor a kitevő páros, és jelöljük 2 · m -rel, ahol m természetes szám.

Ne felejtsük el, hogyan kell helyesen szorozni a negatív számokat: az a · a szorzat egyenlő a modulok szorzatával, és ezért pozitív szám lesz. Akkor  és az a 2 · m fok is pozitív.
és az a 2 · m fok is pozitív.
11. példa
Például (− 6) 4 > 0, (− 2, 2) 12 > 0 és - 2 9 6 > 0
Mi van, ha a negatív bázisú kitevő páratlan szám? Jelöljük 2 · m − 1 .
Akkor 
Minden a · a szorzat a szorzás tulajdonságai szerint pozitív, így a szorzata is. De ha megszorozzuk az egyetlen megmaradt a számmal, akkor a végeredmény negatív lesz.
Ekkor a következőt kapjuk: (− 5) 3< 0 , (− 0 , 003) 17 < 0 и - 1 1 102 9 < 0
Hogyan kell bizonyítani?
a n< b n – неравенство, представляющее собой произведение левых и правых частей nверных неравенств a < b . Вспомним основные свойства неравенств справедливо и a n < b n .
12. példa
Például igazak az egyenlőtlenségek: 3 7< (2 , 2) 7 и 3 5 11 124 > (0 , 75) 124
8. Nekünk marad az utolsó tulajdonság bizonyítása: ha van két fokunk, amelyeknek az alapja azonos és pozitív, és a kitevői természetes számok, akkor közülük az egyik nagyobb, amelynek a kitevője kisebb; és két fok esetén, ahol a természetes mutatók és ugyanazok az alapok nagyobbak, mint egy, az a fok, amelynek a mutatója nagyobb, nagyobb.
Bizonyítsuk be ezeket az állításokat.
Először is meg kell győződnünk arról, hogy egy m< a n при условии, что m больше, чем n , и а больше 0 , но меньше 1 .Теперь сравним с нулем разность a m − a n
A zárójelekből kiveszünk egy n-t, ami után a különbségünk a n · (am − n − 1) alakot ölti. Eredménye negatív lesz (mivel a pozitív szám negatív számmal való szorzata negatív). Valójában a kezdeti feltételek szerint m − n > 0, akkor a m − n − 1 negatív, az első tényező pedig pozitív, mint minden pozitív bázisú természetes hatvány.
Kiderült, hogy a m − a n< 0 и a m < a n . Свойство доказано.
Marad a fent megfogalmazott állítás második részének bizonyítása: a m > a igaz m > n-re és a > 1-re. Jelöljük a különbséget, és a zárójelekből kivesszük az n-t: (a m - n - 1) Egy n hatványa egynél nagyobb pozitív eredményt ad; és maga a különbség is pozitívnak bizonyul a kezdeti feltételek miatt, és a > 1 esetén a m − n foka nagyobb egynél. Kiderült, hogy a m − a n > 0 és a m > a n, amit bizonyítanunk kellett.
13. példa
Példa konkrét számokkal: 3 7 > 3 2
Az egész kitevős fokok alapvető tulajdonságai
Pozitív egész kitevőjű fokok esetén a tulajdonságok hasonlóak lesznek, mivel a pozitív egészek természetes számok, ami azt jelenti, hogy az összes fent bizonyított egyenlőség rájuk is érvényes. Alkalmasak olyan esetekben is, amikor a kitevők negatívak vagy egyenlőek nullával (feltéve, hogy magának a foknak az alapja nem nulla).
Így a hatványok tulajdonságai azonosak bármely a és b bázisra (feltéve, hogy ezek a számok valósak, és nem egyenlők 0-val), valamint bármely m és n kitevőre (feltéve, hogy egész számok). Röviden leírjuk őket képletek formájában:
2. definíció
1. a m a n = a m + n
2. a m: a n = a m − n
3. (a b) n = a n b n
4. (a: b) n = a n: b n
5. (am) n = a m n
6. a n< b n и a − n >b − n pozitív egész számmal n , pozitív a és b , a< b
reggel 7< a n , при условии целых m и n , m >n és 0< a < 1 , при a >1 a m > a n .
Ha a fokszám alapja nulla, akkor az a m és a n bejegyzésnek csak természetes és pozitív m és n esetén van értelme. Ennek eredményeként azt tapasztaljuk, hogy a fenti megfogalmazások a nulla bázisú végzettségű esetekre is megfelelőek, ha minden egyéb feltétel teljesül.
Ezen tulajdonságok bizonyítása ebben az esetben egyszerű. Emlékeznünk kell arra, hogy mi a természetes és egész kitevővel rendelkező fok, valamint a valós számokkal végzett műveletek tulajdonságai.
Elemezzük a fok tulajdonságát a fokban, és bizonyítsuk be, hogy ez mind pozitív, mind nem pozitív egész számokra igaz. Kezdjük az (a p) q = a p q, (a − p) q = a (− p) q, (a p) − q = a p (− q) és (a − p) − q = a (− q) egyenlőségek bizonyításával. p) (-q)
Feltételek: p = 0 vagy természetes szám; q - hasonlóan.
Ha p és q értéke nagyobb, mint 0, akkor azt kapjuk, hogy (a p) q = a p · q . Korábban már bizonyítottunk hasonló egyenlőséget. Ha p = 0, akkor:
(a 0) q = 1 q = 1 a 0 q = a 0 = 1
Ezért (a 0) q = a 0 q
q = 0 esetén minden pontosan ugyanaz:
(a p) 0 = 1 a p 0 = a 0 = 1
Eredmény: (a p) 0 = a p 0.
Ha mindkét mutató nulla, akkor (a 0) 0 = 1 0 = 1 és a 0 0 = a 0 = 1, akkor (a 0) 0 = a 0 0.
Idézzük fel a hányados tulajdonságát a fent bizonyított hatványban, és írjuk be:
1 a p q = 1 q a p q
Ha 1 p = 1 1 … 1 = 1 és a p q = a p q , akkor 1 q a p q = 1 a p q
Ezt a jelölést az alapvető szorzási szabályok alapján átalakíthatjuk a (− p) · q-vé.
Továbbá: a p - q = 1 (a p) q = 1 a p q = a - (p q) = a p (- q) .
ÉS (a - p) - q = 1 a p - q = (a p) q = a p q = a (- p) (- q)
A fok fennmaradó tulajdonságai hasonló módon igazolhatók a meglévő egyenlőtlenségek transzformációjával. Ezzel nem foglalkozunk részletesen, csak a nehéz pontokat jelezzük.
Az utolsó előtti tulajdonság bizonyítása: emlékezzünk arra, hogy a − n > b − n igaz n bármely negatív egészére, valamint bármely pozitív a és b értékére, feltéve, hogy a kisebb, mint b .
Ekkor az egyenlőtlenség a következőképpen alakítható át:
1 a n > 1 b n
Különbségként írjuk a jobb és bal részt, és elvégezzük a szükséges átalakításokat:
1 a n - 1 b n = b n - a n a n b n
Emlékezzünk vissza, hogy abban a feltételben az a kisebb, mint b , akkor a természetes kitevővel rendelkező fok definíciója szerint: - a n< b n , в итоге: b n − a n > 0 .
a n · b n végül pozitív szám lesz, mert faktorai pozitívak. Ennek eredményeként van egy b n - a n a n · b n törtünk, amely végül szintén pozitív eredményt ad. Innen 1 a n > 1 b n a − n > b − n, amit bizonyítanunk kellett.
Az egész kitevős fokok utolsó tulajdonságát a természetes kitevős fokok tulajdonságához hasonlóan igazoljuk.
A fokok alapvető tulajdonságai racionális kitevőkkel
Korábbi cikkeinkben megvitattuk, hogy mi a racionális (tört) kitevővel rendelkező fokozat. Tulajdonságaik megegyeznek az egész kitevővel rendelkező fokokéval. Írjunk:
3. definíció
1. a m 1 n 1 a m 2 n 2 = a m 1 n 1 + m 2 n 2 ha a > 0, és ha m 1 n 1 > 0 és m 2 n 2 > 0, akkor a ≥ 0 esetén (terméktulajdonság-hatványok ugyanazzal az alappal).
2. a m 1 n 1: b m 2 n 2 = a m 1 n 1 - m 2 n 2, ha a > 0 (hányados tulajdonság).
3. a b m n = a m n b m n a > 0 és b > 0 esetén, és ha m 1 n 1 > 0 és m 2 n 2 > 0, akkor a ≥ 0 és (vagy) b ≥ 0 esetén (a szorzati tulajdonság tört fokban).
4. a: b m n \u003d a m n: b m n, ha a > 0 és b > 0, és ha m n > 0, akkor a ≥ 0 és b > 0 esetén (egy hányados tulajdonsága egy törthatványhoz).
5. a m 1 n 1 m 2 n 2 \u003d am 1 n 1 m 2 n 2 ha a > 0, és ha m 1 n 1 > 0 és m 2 n 2 > 0, akkor a ≥ 0 esetén (foktulajdonság fok).
6.ap< b p при условии любых положительных a и b , a < b и рациональном p при p >0; ha p< 0 - a p >b p (a fokok egyenlő racionális kitevőkkel való összehasonlításának tulajdonsága).
7.ap< a q при условии рациональных чисел p и q , p >q 0-nál< a < 1 ; если a >0 – a p > a q
E rendelkezések bizonyításához emlékeznünk kell arra, hogy mi az a fokszám tört kitevővel, milyen tulajdonságai vannak az n-edik fokú számtani gyöknek, és melyek az egész kitevővel rendelkező fok. Vessünk egy pillantást az egyes ingatlanokra.
Aszerint, hogy mi a fokszám tört kitevővel, a következőket kapjuk:
a m 1 n 1 = 1 n 1 és a m 2 n 2 \u003d am 2 n 2, tehát a m 1 n 1 a m 2 n 2 \u003d am 1 n 1 a m 2 n 2
A gyökér tulajdonságai lehetővé teszik, hogy egyenlőségeket származtassunk:
a m 1 m 2 n 1 n 2 a m 2 m 1 n 2 n 1 = a m 1 n 2 a m 2 n 1 n 1 n 2
Ebből a következőt kapjuk: a m 1 n 2 a m 2 n 1 n 1 n 2 = a m 1 n 2 + m 2 n 1 n 1 n 2
Alakítsuk át:
a m 1 n 2 a m 2 n 1 n 1 n 2 = a m 1 n 2 + m 2 n 1 n 1 n 2
A kitevő a következőképpen írható fel:
m 1 n 2 + m 2 n 1 n 1 n 2 = m 1 n 2 n 1 n 2 + m 2 n 1 n 1 n 2 = m 1 n 1 + m 2 n 2
Ez a bizonyíték. A második tulajdonság pontosan ugyanígy bizonyított. Írjuk fel az egyenlőségláncot:
a m 1 n 1: a m 2 n 2 = a m 1 n 1: a m 2 n 2 = a m 1 n 2: a m 2 n 1 n 1 n 2 = = a m 1 n 2 - m 2 n 1 n 1 n 2 = a m 1 n 2 - m 2 n 1 n 1 n 2 = a m 1 n 2 n 1 n 2 - m 2 n 1 n 1 n 2 = a m 1 n 1 - m 2 n 2
A fennmaradó egyenlőségek bizonyítékai:
a b m n = (a b) m n = a m b m n = a m n b m n = a m n b m n ; (a: b) m n = (a: b) m n = a m: b m n = = a m n: b m n = a m n: b m n ; a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = = a m 1 m 2 n 1 n 2 = a m 1 m 2 n 1 n 2 = = a m 1 m 2 n 2 n 1 = a m 1 m 2 n 2 n 1 = a m 1 n 1 m 2 n 2
Következő tulajdonság: bizonyítsuk be, hogy a és b bármely 0-nál nagyobb értékére, ha a kisebb, mint b, akkor a p kerül végrehajtásra< b p , а для p больше 0 - a p >bp
Egy p racionális számot ábrázoljunk m n -ként. Ebben az esetben m egész szám, n természetes szám. Ezután a feltételek p< 0 и p >0 ki lesz terjesztve m-re< 0 и m >0 . m > 0 és a< b имеем (согласно свойству степени с целым положительным показателем), что должно выполняться неравенство a m < b m .
Használjuk a gyökök tulajdonságát, és származtatjuk: a m n< b m n
Figyelembe véve az a és b értékek pozitívságát, az egyenlőtlenséget a m n-re írjuk át< b m n . Оно эквивалентно a p < b p .
Ugyanígy a m< 0 имеем a a m >b m , a m n > b m n tehát a m n > b m n és a p > b p értéket kapjuk.
Nekünk marad az utolsó tulajdonság bizonyítása. Bizonyítsuk be, hogy p és q racionális számokra p > q 0-nál< a < 1 a p < a q , а при a >0 igaz lenne a p > a q .
A p és q racionális számok közös nevezőre redukálhatók és m 1 n és m 2 n törteket kapunk
Itt m 1 és m 2 egész számok, n pedig természetes szám. Ha p > q, akkor m 1 > m 2 (figyelembe véve a törtek összehasonlításának szabályát). Aztán 0-nál< a < 1 будет верно a m 1 < a m 2 , а при a >1 – egyenlőtlenség a 1 m > a 2 m .
Átírhatók a következő formában:
a m 1 n< a m 2 n a m 1 n >a m 2 n
Ezután átalakításokat hajthat végre, és az eredmény:
a m 1 n< a m 2 n a m 1 n >a m 2 n
Összefoglalva: p > q és 0 esetén< a < 1 верно a p < a q , а при a >0 – a p > a q .
A fokok alaptulajdonságai irracionális kitevőkkel
Az összes fent leírt tulajdonság, amellyel egy racionális kitevővel rendelkező fok rendelkezik, kiterjeszthető ilyen fokra. Ez a meghatározásából következik, amelyet az egyik korábbi cikkben adtunk meg. Fogalmazzuk meg röviden ezeket a tulajdonságokat (feltételek: a > 0, b > 0, a p és q mutatók irracionális számok):
4. definíció
1. a p a q = a p + q
2. a p: a q = a p − q
3. (a b) p = a p b p
4. (a: b) p = a p: b p
5. (a p) q = a p q
6.ap< b p верно при любых положительных a и b , если a < b и p – иррациональное число больше 0 ; если p меньше 0 , то a p >bp
7.ap< a q верно, если p и q – иррациональные числа, p < q , 0 < a < 1 ; если a >0 , majd a p > a q .
Így minden olyan hatvány, amelynek p és q kitevője valós szám, azonos tulajdonságokkal rendelkezik, feltéve, hogy a > 0.
Ha hibát észlel a szövegben, jelölje ki, és nyomja meg a Ctrl+Enter billentyűkombinációt
algebra 7. osztály
matematika tanár
ág MBOUTSOSH №1
Poletaevo Zueva I.P. faluban.
Poletaevo 2016
Tantárgy: « Fokozat tulajdonságai természetes kitevővel»
CÉL
- A tanult anyag ismétlése, általánosítása, rendszerezése a „természetes mutatójú végzettség tulajdonságai” témában.
- A tanulók tudásának ellenőrzése a témában.
- Az elsajátított ismeretek alkalmazása a különböző feladatok ellátása során.
FELADATOK
tantárgy :
megismételni, általánosítani és rendszerezni a témával kapcsolatos ismereteket; feltételeket teremteni a tudás és készségek asszimilációjának ellenőrzéséhez (kölcsönös ellenőrzéséhez);folytassa a tanulók motivációjának kialakítását a tantárgy tanulására;
metatárgy:
operatív gondolkodásmód kialakítása; elősegíteni a tanulók kommunikációs készségek elsajátítását a közös munka során; aktiválják kreatív gondolkodásukat; Pa tanulók bizonyos kompetenciáinak kialakításának folytatása, ami hozzájárul hatékony szocializációjukhoz;önképzési és önképzési készségek.
személyes:
kultúra nevelése, az egymáshoz, az emberekhez, az élethez való jóindulatú, toleráns magatartást célzó személyes tulajdonságok kialakulásának elősegítése; a tevékenységekben a kezdeményezés és a függetlenség ápolása; annak megértéséhez, hogy a vizsgált témára van szükség az állami záróbizonyítványra való sikeres felkészüléshez.
ÓRATÍPUS
általánosítás és rendszerezés óra ZUN.
Felszerelés: számítógép, projektor,vetítővászon,tábla, szórólap.
Szoftver: Windows 7 operációs rendszer: MS Office 2007 (szükséges jelentkezés - powerpoint).
Előkészületi szakasz:
előadás "A diploma tulajdonságai naturális mutatóval";
Kiosztóanyag;
pontozólap.
Szerkezet
Idő szervezése. Az óra céljainak és célkitűzéseinek meghatározása - 3 perc.
Az alapismeretek aktualizálása, rendszerezése - 8 perc.
Gyakorlati rész - 28 perc.
Általánosítás, következtetés -3 perc.
Házi feladat- 1 perc.
Reflexió - 2 perc.
Óra ötlet
Érdekes és hatékony módon ellenőrizni a hallgatók ZUN-ját ebben a témában.
Az óra szervezése Az órát a 7. osztályban tartják. A gyerekek párban, önállóan dolgoznak, a tanár tanácsadó-megfigyelőként tevékenykedik.
Az órák alatt
Szervezési idő:
Helló srácok! Ma egy rendhagyó lecke-játékunk van. Mindannyian nagyszerű lehetőséget kapnak, hogy bizonyítsanak, megmutassák tudásukat. Talán az óra során olyan rejtett képességeket fedezel fel magadban, amelyek hasznosak lesznek számodra a jövőben.
Mindenkinek van egy tesztlapja és a feladatok elvégzéséhez szükséges kártyák. Vegyen a kezébe egy tesztlapot, szüksége van rá, hogy maga értékelje tudását az órán. Írd alá.
Szóval meghívlak a leckére!
Srácok, nézzétek a képernyőt és hallgassátok a verset.
1. dia
Szorozni és osztani
Erőt hatalommá emelni...
Ismerjük ezeket a tulajdonságokat.
És már nem újak.
Ez az öt egyszerű szabály
Az osztályból már mindenki válaszolt
De ha elfelejtette a tulajdonságokat,
Tekintse meg azt a példát, amelyet nem oldott meg!
És azért, hogy az iskolában gond nélkül élhessünk
Adok egy jó tanácsot:
El akarod felejteni a szabályt?
Próbálj csak tanulni!
Válaszold meg a kérdést:
1) Milyen cselekvések szerepelnek benne?
2) Mit gondolsz, miről fogunk ma beszélni a leckén?
Tehát óránk témája:
"Fokozat tulajdonságai természetes kitevővel" (3. dia).
Az óra céljainak és célkitűzéseinek meghatározása
A leckében megismételjük, összefoglaljuk és rendszerbe hozzuk a „Fokozat tulajdonságai természetes indikátorral” témában tanult anyagot.
Lássuk, hogyan tanultad meg a hatványok szorzását és osztását ugyanazzal az alappal, valamint hogyan emelhetsz hatványt hatványra
Az alapismeretek frissítése. Elméleti anyag rendszerezése.
1) Szóbeli munka
Dolgozzunk verbálisan
1) Fogalmazza meg a fok tulajdonságait természetes jelzővel!
2) Töltse ki az üres helyeket: (4. dia)
1)5 12 : 5 5 =5 7 2) 5 7 ∙ 5 17 = 5 24 3) 5 24 : 125= 5 21 4)(5 0 ) 2 ∙5 24 =5 24
5)5 12 ∙ 5 12 = (5 8 ) 3 6)(3 12 ) 2 = 3 24 7) 13 0 ∙ 13 64 = 13 64
3) Mi a kifejezés értéke:(5-9. dia)
a m ∙ a n; (a m+n ) a m : a n (a m-n ) ; (a m ) n; a 1; és 0 .
2) Az elméleti rész ellenőrzése (1. kártya)
Most vegye fel az 1-es számú kártyát éstöltse ki a hézagokat
1) Ha a mutató páros szám, akkor a fok értéke mindig _______________
2) Ha a mutató páratlan szám, akkor a fok értéke egybeesik a ____ előjellel.
3) Hatványok szorzata a n a k = a n + k
Ha a hatványokat ugyanazzal az alappal szorozzuk meg, a ____________ alapra és a ________ kitevőkre van szükség.
4) Magándiplomák a n : a k = a n - k
Ha a hatványokat azonos alappal osztjuk fel, akkor a _____ bázisra van szükség, az osztalék mutatójából pedig a _________________________________.
5) Fokozat hatványra emelése ( a n ) k = a nk
Ha egy hatványt hatványra emelünk, az alap _______, a kitevők pedig ______.
Válaszok ellenőrzése. (10-13. dia)
Fő rész
3) És most kinyitjuk a füzeteket, felírjuk a 28.01 14g számot, órai munka
A "Clapperboard" játék » (14. dia)
Végezze el önállóan a füzeteiben található feladatokat
Tedd a következőket: a)x11 ∙х∙х2 b)x14 : X5 c) (a4 ) 3 d) (-For)2 .
Hasonlítsa össze a kifejezés értékét nullával: a) (- 5)7 , b)(-6)18 ,
4-nél)11 . ( -4) 8 G)(- 5) 18 ∙ (- 5) 6 , e)-(- 4)8 .
Számítsa ki egy kifejezés értékét:
a) -1 ∙ 3 2, b) (-1 ∙ 3) 2 c) 1 ∙ (-3) 2, d) - (2 ∙ 3) 2, e) 1 2 ∙ (-3) 2
Ellenőrizzük, ha nem helyes a válasz, egyet tapsolunk.
Számold ki a pontok számát, és írd fel a pontozólapra!
4) És most tornázzuk a szemeket, oldjuk a feszültséget, és folytatjuk a munkát. Gondosan figyeljük a tárgyak mozgását
Kezdődik! (15.,16.,17.,18. dia).
5) És most folytassuk munkánk következő típusát. (2. kártya)
Írja le a válaszát, mint egy bázissal rendelkező erőt VAL VEL és megtanulod a nagy francia matematikus nevét és vezetéknevét, aki elsőként vezette be a szám fokának fogalmát.
Találd ki a tudós matematikus nevét.
| 1. | VAL VEL 5 ∙С 3 | 6. | VAL VEL 7 : VAL VEL 5 |
| 2. | VAL VEL 8 : VAL VEL 6 | 7. | (VAL VEL 4 ) 3 ∙С |
| 3, | (VAL VEL 4 ) 3 | 8. | VAL VEL 4 ∙ VAL VEL 5 ∙ C 0 |
| 4. | VAL VEL 5 ∙С 3 : VAL VEL 6 | 9. | VAL VEL 16 : VAL VEL 8 |
| 5. | VAL VEL 14 ∙ C 8 | 10. | (VAL VEL 3 ) 5 |
RÓL RŐL Válasz: RENE DECARTES
| R | W | M | YU | NAK NEK | H | A | T | E | D |
|||||
| VAL VEL 8 | VAL VEL 5 | VAL VEL 1 | VAL VEL 40 | VAL VEL 13 | VAL VEL 12 | VAL VEL 9 | VAL VEL 15 | VAL VEL 2 | VAL VEL 22 |
És most hallgassuk meg a diák üzenetét "Rene Descartes"-ról
Rene Descartes 1596. március 21-én született a tourainei La Gaie kisvárosban. A Descartes család a szerény bürokratikus nemességhez tartozott. Rene gyerekkorát Touraine-ban töltötte. Descartes 1612-ben fejezte be az iskolát. Nyolc és fél évet töltött ott. Descartes nem találta meg azonnal a helyét az életben. Született nemes, miután elvégezte a La Fleche-i főiskolát, hanyatt-homlok zuhan Párizs társasági életébe, majd a tudomány kedvéért mindent felad. Descartes a matematikának különleges helyet adott rendszerében, az igazság megállapításának elveit más tudományok mintájának tekintette. Descartes jelentős érdeme volt a máig fennmaradt kényelmes elnevezések bevezetése: a latin x, y, z betűk az ismeretlenekre; a, c, c - együtthatókhoz, fokokhoz. Descartes érdeklődési köre nem korlátozódik a matematikára, hanem magában foglalja a mechanikát, az optikát és a biológiát is. 1649-ben Descartes hosszas habozás után Svédországba költözött. Ez a döntés végzetesnek bizonyult az egészségére nézve. Hat hónappal később Descartes tüdőgyulladásban meghalt.
6) Munka a testületnél:
1. Oldja meg az egyenletet
A) x 4 ∙ (x 5) 2 / x 20: x 8 \u003d 49
B) (t 7 ∙ t 17 ): (t 0 t 21 )= -125
2.Számítsa ki a kifejezés értékét:
(5-x) 2 -2x3 +3x 2 -4x+x-x 0
a) x=-1-nél
b) x=2-nél Függetlenül
7) Vedd a kezedbe a 3-as számú kártyát, és végezd el a tesztet
| választási lehetőség 1 | 2. lehetőség. |
| 1. Végezze el a hatáskörök megosztását 2 17 : 2 5 2 12 2 45 2. Írja be fok alakban (x + y) (x + y) \u003d x 2 + y 2 (x+y) 2 2(x+y) 3. Cserélje ki * fokát úgy, hogy az egyenlőség a 5 · * =a 15 egy 10 a 3 (a 7 ) 5 ? a) a 12 b) a 5 c) a 35 3 = 8 15 8 12 6. Határozza meg a tört értékét! | 1. Oszd el a 9 hatványaival 9 : 9 7 9 16 9 63 2. Írja fok (x-y) (x-y) \u003d ... x 2 -y 2 (x-y) 2 2 (x-y) 3. Cserélje ki * fokon úgy, hogy az egyenlőség b 9 · * = b 18 b 17 b 1 1 4. Mi a kifejezés értéke(6-tal) 4 ? a) 10-től b) 6-tól c) 24-től 5. A javasolt lehetőségek közül válassza ki azt, amelyik helyettesítheti a *-t egyenlőségben (*) 3 = 5 24 5 21 6. Határozza meg a tört értékét! |
Ellenőrizzék egymás munkáját, és értékeljék a bajtársakat az osztályzatlapon.
| 1 lehetőség | A | b | b | Val vel | b | 3 |
| 2. lehetőség | A | b | Val vel | Val vel | A | 4 |
További feladatok erős tanulóknak
Minden feladatot külön értékelünk.
Keresse meg egy kifejezés értékét:
8) És most lássuk leckénk hatékonyságát ( 19. dia)
Ehhez hajtsa végre a feladatot, húzza ki a válaszoknak megfelelő betűket.
AOWSTLCCRCHGNMO
Egyszerűsítse a kifejezést:
| 1. | С 4 ∙С 3 | 5. | (VAL VEL 2 ) 3 ∙ VAL VEL 5 |
| 2. | (C 5 ) 3 | 6. | VAL VEL 6 ∙ VAL VEL 5 : VAL VEL 10 |
| 3. | 11-től: 6-tól | 7. | (VAL VEL 4 ) 3 ∙С 2 |
| 4. | C 5 ∙ C 5 : C |
Rejtjel: A - 7-től BAN BEN- 15-től G - VAL VEL ÉS - 30-tól NAK NEK - 9-től M - 14-től H - 13-tól RÓL RŐL - 12-től R - 11-től VAL VEL - 5-től T - 8-tól H - 3-tól
Milyen szót kaptál? VÁLASZ: KIVÁLÓ! (20. dia)
Összegzés, értékelés, jelölés (21. dia)
Foglaljuk össze leckénket, hogy milyen sikeresen ismételtük, általánosítottuk, rendszereztük a „természetes mutatójú végzettség tulajdonságai” témában szerzett ismereteket.
Tesztlapokat veszünk és kiszámoljuk az összpontszámot, és felírjuk a végső osztályzat sorába
Álljon fel, aki 29-32 pontot szerzett: kiváló eredmény
25-28 pont: pontszám - jó
20-24 pont: pontszám - kielégítő
Még egyszer ellenőrizni fogom a kártyákon szereplő feladatok helyességét, a tesztlapon beállított pontokkal ellenőrzöm az eredményeiteket. Az osztályzatokat beírom a naplóba
És az értékelő órán való aktív munkához:
Gyerekek, arra kérlek benneteket, hogy értékeljék a leckében végzett munkájukat. Jelöld a hangulatlapon.
| Tesztlap |
||
| Vezetéknév Keresztnév | Fokozat |
|
| 1. Elméleti rész | ||
| 2. "Clapperboard" játék | ||
| 3. Teszt | ||
| 4. "Rejtjel" | ||
| Kiegészítő rész | ||
| Végső osztályzat: | ||
| Érzelmi értékelés | Rólam | A leckéről |
| Elégedett | ||
| elégedetlen | ||
Házi feladat (22. dia)
Készíts keresztrejtvényt ezzel kulcsszó FOKOZAT. A következő leckében a legérdekesebb munkákat nézzük meg.
№ 567
A felhasznált források listája
- Tankönyv "Algebra 7. évfolyam".
- Vers. http://yandex.ru/yandsearch
- NEM. Scsurkov. A modern óra kultúrája. Moszkva: Orosz Pedagógiai Ügynökség, 1997.
- A.V. Petrov. A személyiségfejlesztő számítógépes oktatás módszertani és módszertani alapjai. Volgográd. "Változás", 2001.
- MINT. Belkin. sikerhelyzet. Hogyan kell létrehozni. M .: "Felvilágosodás", 1991.
- Számítástechnika és oktatás №3. Operatív gondolkodási stílus, 2003
Az óra típusa: az ismeretek általánosításának és rendszerezésének órája
Az óra típusa: kombinált
Munkaformák: egyéni, frontális, páros munka
Felszerelés: számítógép, médiatermék (bemutató a programbanMicrosofthivatalpower point 2007); feladatkártyák önálló tanuláshoz
Az óra céljai:
Nevelési : a fokozattal kapcsolatos ismeretek naturális jelzővel történő rendszerezésének, általánosításának, a fokozatokat tartalmazó kifejezések természetes jelzővel történő legegyszerűbb transzformációinak készségeinek megszilárdítása, fejlesztése.
- fejlesztés: elősegíteni az általánosítás, összehasonlítás módszereinek alkalmazására alkalmas készségek kialakulását, a legfontosabb kiemelést, a matematikai látókör, a gondolkodás, a beszéd, a figyelem és a memória fejlesztését.
- oktatási: a matematika, tevékenység, szervezés iránti érdeklődés oktatásának elősegítése, pozitív motiváció kialakítása a tanuláshoz, az oktatási és kognitív tevékenységhez szükséges készségek fejlesztéséhez
Magyarázó jegyzet.
Ezt az órát egy átlagos matematikai felkészültségű általános műveltségi osztályban tartják. Az óra fő feladata a fokozattal kapcsolatos ismeretek rendszerezési, általánosítási képességeinek fejlesztése egy természetes mutatóval, amely a különböző gyakorlatok végrehajtása során valósul meg.
A fejlesztő jelleg a gyakorlatok kiválasztásában nyilvánul meg. A multimédiás termék használatával időt takaríthat meg, vizuálisabbá teheti az anyagot, mintákat mutathat be a tervezési megoldásokból. különböző fajták működik, ami enyhíti a gyerekek fáradtságát.
Az óra felépítése:
Idő szervezése.
Üzenettéma, az óra céljainak kitűzése.
szóbeli munka.
Az alapismeretek rendszerezése.
Az egészségmegőrző technológiák elemei.
Tesztfeladat végrehajtása
Az óra eredményei.
Házi feladat.
Az órák alatt:
én.Időszervezés
Tanár: Sziasztok srácok! Örülök, hogy üdvözölhetem a mai óránk. Ülj le. Remélem, hogy a mai órán sikerrel és örömmel is lesz részünk. Mi pedig csapatban dolgozva megmutatjuk tehetségünket.
Legyen óvatos az óra alatt. Gondolkozz, kérj, kínálj – hiszen együtt járjuk az igazsághoz vezető utat.
Nyissa ki a füzeteket, és írja le a számot, az órai munkát
II. Témaüzenet, órai cél kitűzése
1) Az óra témája. Az óra epigráfiája.(2.3. dia)
– Próbáljon valaki áthúzni a matematikából
fokozatot, és látni fogja, hogy nélkülük nem jutsz messzire” M.V. Lomonoszov
2) Az óra célkitűzéseinek meghatározása.
Tanár: Tehát a leckében megismételjük, összefoglaljuk és bevisszük a rendszerbe a tanult anyagot. Feladata, hogy egy naturális jelzővel mutassa meg tudását a diploma tulajdonságairól, és azok alkalmazásának képességét különböző feladatok elvégzése során.
III. A témakör alapfogalmainak, a diploma tulajdonságainak megismétlése természetes mutatóval
1) fejtsd ki az anagrammát: (4. dia)
Nspete (fok)
Kurvárgás (vágás)
Ovaniosne (alap)
Casapotel (jelző)
Szorzás (szorzás)
2) Mi a természetes mutatójú diploma?(5. dia)
(a szám erejével a természetes indikátorral n , nagyobb, mint 1, kifejezésnek nevezzük a n egyenlő a termékkel n szorzók, amelyek mindegyike egyenlő a megaláz n -index)
3) Olvassa el a kifejezést, nevezze meg az alapot és a kitevőt: (6. dia)
4) A fokozat alapvető tulajdonságai (adjuk hozzá az egyenlőség jobb oldalát)(7. dia)
a n a m =
a n :a m =
(a n ) m =
(ab) n =
( a / b ) n =
a 0 =
a 1 =
IV Nál nél stnaya Munka
1) szóbeli beszámoló (8. dia)
Tanár: És most nézzük meg, hogyan tudod alkalmazni ezeket a képleteket a megoldás során.
1)x 5 x 7 ; 2) a 4 A 0 ;
3) hogy 9 : Nak nek 7 ; 4) r n : r ;
5)5 5 2 ; 6) (- b )(- b ) 3 (- b );
7) -val 4 : Val vel; 8) 7 3 : 49;
9) 4 nál nél 6 y 10) 7 4 49 7 3 ;
11) 16: 4 2 ; 12) 64: 8 2 ;
13) sss 3 ; 14) a 2 n a n ;
15) x 9 : X m ; 16) at n : y
2) a "Kizárja a felesleget" játék ((-1) 2 )(9. dia)
-1
Szép munka. Jó munkát végeztek. Ezután a következő példákat oldjuk meg.
VAz alapismeretek rendszerezése
1. Kösd össze az egymásnak megfelelő kifejezéseket vonalakkal:(10. dia)
4 ⁶ 4 2 3 6 4 6
4 6 : 4 2 4 6 /5 6
(3 4) 6 4 ⁶ +2
(4 2 ) 6 4 6-2
(4/5) 6 4 12
2. Rendezd a szám szerint növekvő sorrendbe:(11. dia)
3 2 (-0,5) 3 (½) 3 35 0 (-10) 3
3. A feladat elvégzése utólagos önvizsgálattal(12. dia)
Az A1 a terméket diploma formájában jelöli:
a) a) x 5 x 4 ; b) 3 7 3 9 ; 4-kor) 3 (-4) 8 .
És 2 egyszerűsíti a kifejezést:
a) x 3 x 7 x 8 ; b) 2 21 :2 19 2 3
És 3 hatványozás:
a) (a 5 ) 3 ; időszámításunk előtt 7 ) 2
VIEgészségvédő technológiák elemei (13. dia)
Testnevelés: a 2-es és 3-as számfokozat ismétlése
 VIITesztfeladat (14. dia)
VIITesztfeladat (14. dia)
A tesztre adott válaszok fel vannak írva a táblára: 1 d 2 o 3b 4s 5 h 6a (kivonás)
VIII Önálló munka kártyákon
Minden asztalon lehetőség szerinti feladattal ellátott kártyák, a munka elvégzése után ellenőrzésre kerülnek
1.opció
1) Egyszerűsítse a kifejezéseket:
A)  b)
b) 
V)  G)
G) 
A)  b)
b) 
V)  G)
G)
2. lehetőség
1) Egyszerűsítse a kifejezéseket:
A) b)
V)  G)
G)
2) Keresse meg a kifejezés értékét:
A)b)
V)  G)
G) 
3) Mutasd meg nyíllal, hogy a kifejezés értéke nullával, pozitív vagy negatív számmal egyenlő-e:
IX Óraösszefoglaló
sz. p / p
Munka típusa
önbecsülés
Tanári értékelés
1
Anagramma
2
Olvasd el a kifejezést
3
Szabályok
4
Verbális számolás
5
Csatlakozás vonalakkal
6
Rendezd növekvő sorrendbe
7
Önellenőrző feladatok
8
Teszt
9
Önálló munka kártyákkal
X Házi feladat
Tesztkártyák
A1. Keresse meg a kifejezés értékét: .
Lecke a témában: "A fokozat és tulajdonságai."
Az óra célja:
Foglalja össze a tanulók tudását a következő témában: „Fokozat természetes mutatóval”.
Elérni a hallgatóktól a fokozat meghatározásának tudatos megértését, a tulajdonságokat, azok alkalmazásának képességét.
Megtanítani az ismeretek, készségek alkalmazását különböző összetettségű feladatokhoz.
Teremtse meg az önállóság, a kitartás, a szellemi aktivitás megnyilvánulásának feltételét, nevelje a matematika szeretetét.
Felszerelés: lyukkártyák, kártyák, tesztek, asztalok.
Az óra célja, hogy rendszerezze és általánosítsa a hallgatók tudását egy természetes mutató segítségével a diploma tulajdonságairól. Az óra anyaga matematikai ismereteket formál a gyerekekben és fejleszti a tantárgy iránti érdeklődést, történelmi vonatkozásban a horizontot.
Előrehalad.
Üzenet az óra témájával és céljával kapcsolatban.
Ma van egy általános leckénk a "Fokozat természetes indikátorral és tulajdonságaival" témában.
Leckénk feladata az összes feldolgozott anyag megismétlése és felkészülés a tesztre.
Házi feladat ellenőrzése.
(Cél: a hatványozás, a szorzat és a fokozat elsajátításának ellenőrzése).
№ 238. b) pont 220. a; d) 216. sz.
A tábla mögött 2 személy van egyéni kártyákkal.
a 4 ∙ a 15 a 12 ∙ a 4 a 12: a 4 a 18: a 9 (a 2) 5 (a 4) 8 (a 2 b 3) 6 (а 6 bв 4) 3 a 0 a 0szóbeli munka.
(Cél: megismételni azokat a kulcspontokat, amelyek megerősítik a hatványok szorzó- és osztó algoritmusát, a hatványozást).
Fogalmazza meg egy szám fokszámának meghatározását természetes kitevővel!
Cselekszik.
Mekkora x értéknél áll fenn az egyenlet?
Határozza meg a kifejezés előjelét számítások elvégzése nélkül.
Egyszerűsítsd.
 ; b) (a 4) 6:
(a 3) 3
; b) (a 4) 6:
(a 3) 3 Ötletelés.
( Cél : ellenőrizze a hallgatók alapismereteit, a diploma tulajdonságait).
Dolgozzon lyukkártyákkal a gyorsaság érdekében.
 a 6: a 4; a 10: a 3
(a 2) 2;
(a 3) 3; (a 4) 5; (а 0) 2 .
a 6: a 4; a 10: a 3
(a 2) 2;
(a 3) 3; (a 4) 5; (а 0) 2 . - (2а 2) 2;
(-2a 3) 3; (3а 4) 2; (-2a 2 b) 4 .
Gyakorlat: A kifejezés egyszerűsítése (párban dolgozunk, az osztály az a, b, c feladatot oldja meg, közösen ellenőrizzük).
(Cél: egy fokozat tulajdonságainak kidolgozása természetes mutatóval.)
A)  ; b)
; b)  ; V)
; V) 
6. Kiszámítja:
A)  ( együttesen )
( együttesen )
b)  ( egymaga )
( egymaga )
V)  ( egymaga )
( egymaga )
G) 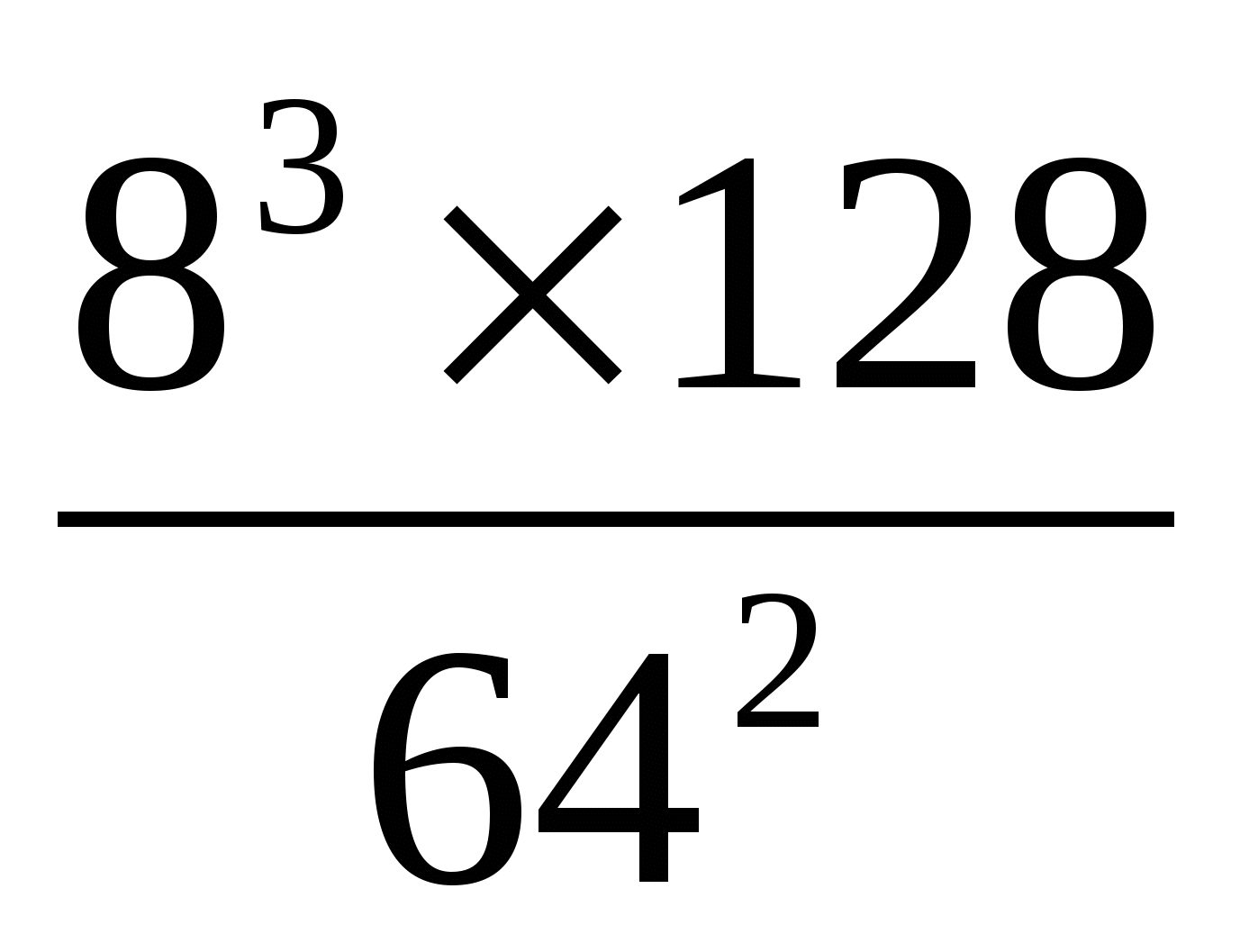 ( együttesen )
( együttesen )
e)  ( egymaga ).
( egymaga ).
7 . Ellenőrizd le magadat!
(Cél: a tanulók alkotótevékenysége elemeinek és cselekvéseik irányításának képességének fejlesztése).
Munka tesztekkel, 2 tanuló a táblánál, önvizsgálat.
I - c.


Kifejezések kiszámítása.
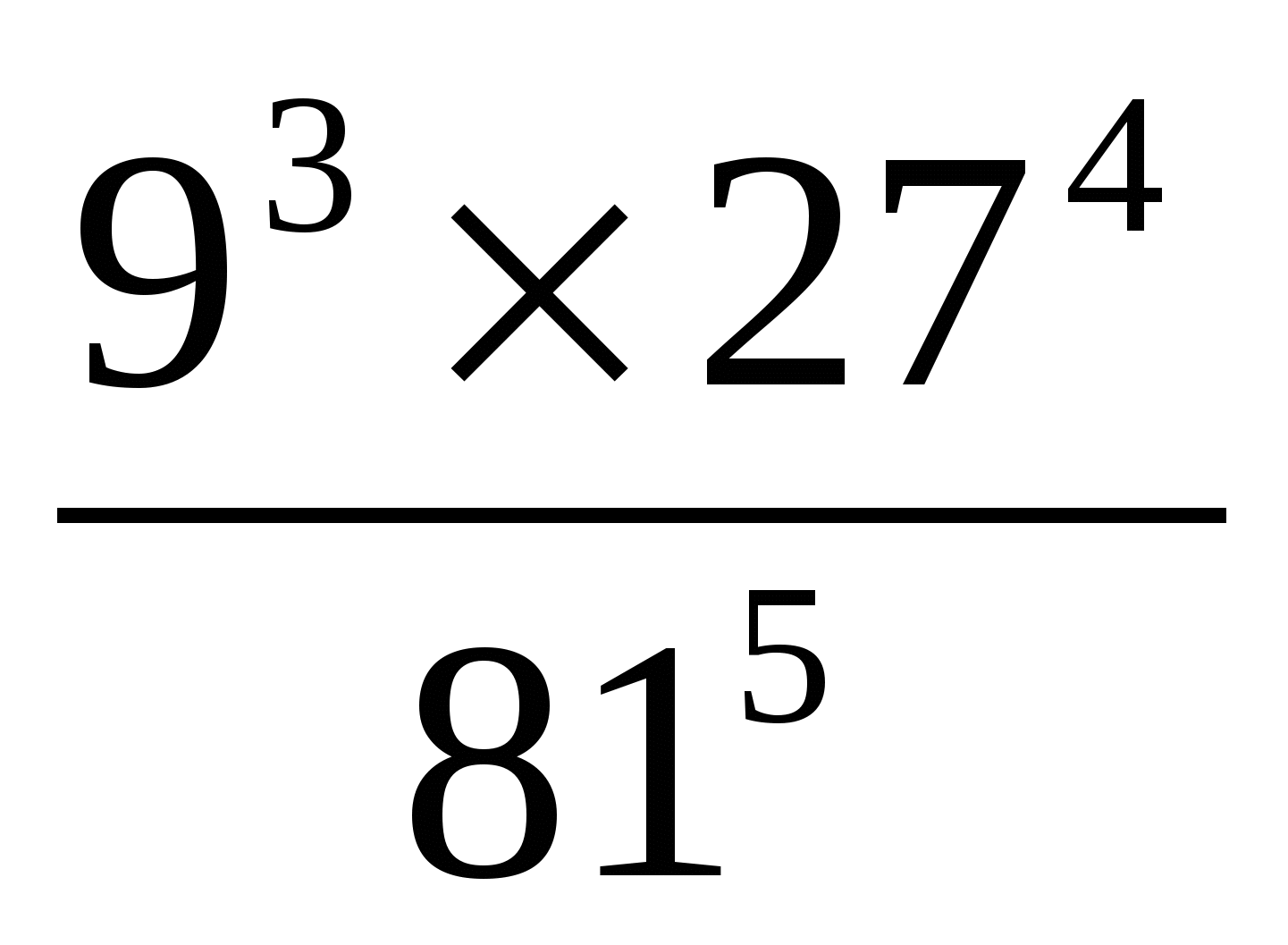
║ - V.
A kifejezések egyszerűsítése.

Kiszámítja.

Kifejezések kiszámítása.
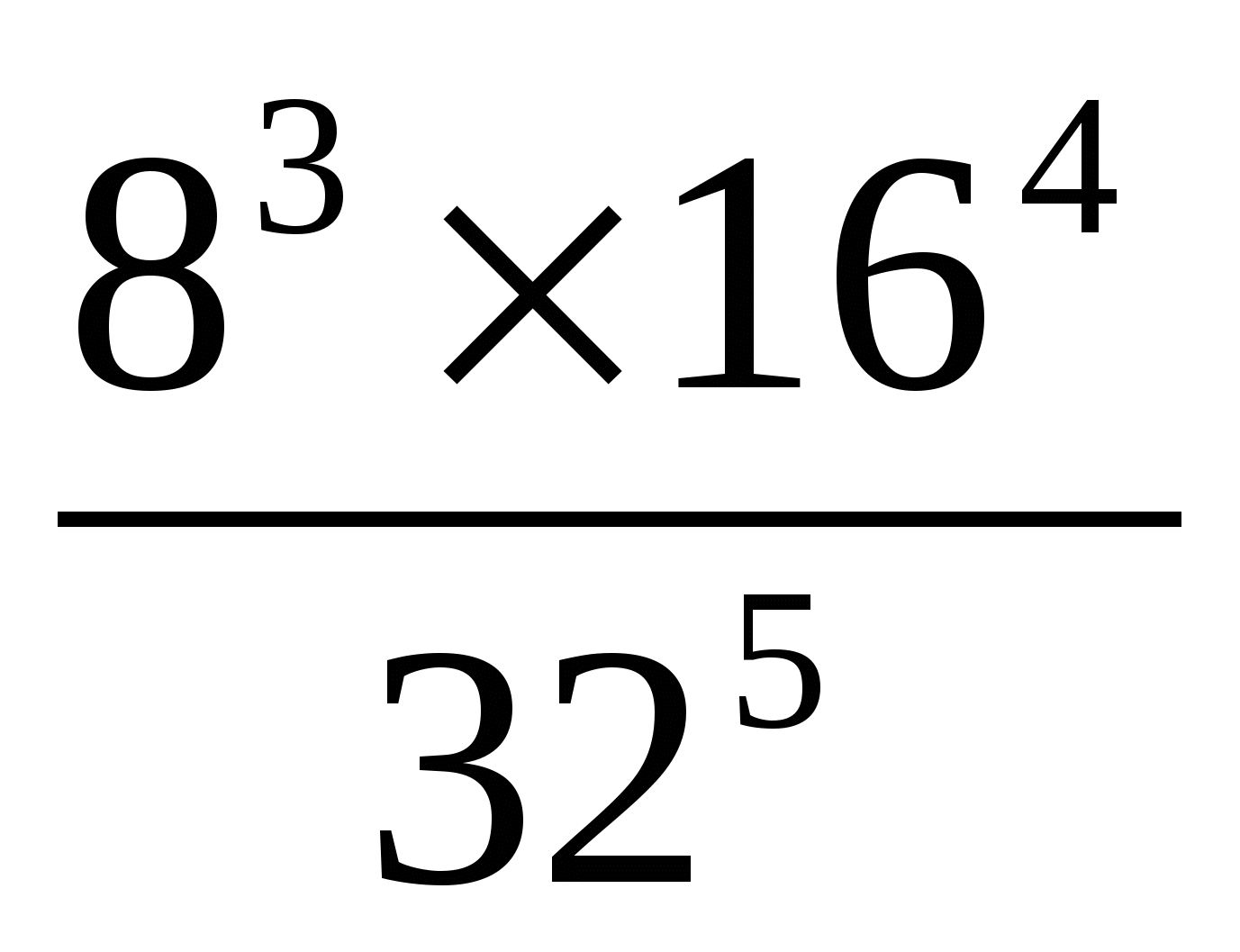
D / s haza / r (kártyákon).
Óra összegzése, osztályozás.
(Cél: Hogy a tanulók vizuálisan lássák munkájuk eredményét, fejlődjön a kognitív érdeklődés).
Ki kezdte el először a diplomát?
Hogyan neveljünk n ?
Tehát az n-edik fokig miA egyenesen
Meg kell szoroznunk n-t egyszer
Ha n egy – soha
Ha több, akkor szorozzuk a on a,
ismétlem n-szer.
3) Emelhetünk-e egy számot n fok, nagyon gyors?
Ha veszel egy számológépet
Szám a csak egyszer kapod meg
És akkor a "szorzás" jele - szintén egyszer,
Annyiszor fogod megnyomni a "kiderül" táblát
Mennyi n egység nélkül megmutatja nekünk
És kész a válasz, iskolai toll nélkül MÉG .
4) Sorolja fel a fok tulajdonságait természetes jelzővel!
Az óra osztályzatait a munka lyukkártyás ellenőrzése után, tesztekkel állítjuk fel, figyelembe véve azon tanulók válaszait, akik az órán válaszoltak.
Jó munkát végeztél ma, köszönöm.
Irodalom:
1.A.G. Mordkovich Algebra-7 osztály.
2.Didaktikai anyagok – 7. évfolyam.
3.A.G. Mordkovich tesztek – 7. osztály.

