Nem megfelelő integrálok konvergenciája és divergenciája. Hogyan lehet kiszámítani egy nem megfelelő integrált és megtudni a konvergenciáját. A konvergencia jelei. Abszolút és feltételes konvergencia
Példák a nem megfelelő integrálok tanulmányozására a konvergenciához
1. példa
 .
.
Így ez az integrál a>1 esetén konvergál, és £1 esetén divergál.
2. példa
Vizsgálja meg a konvergenciát. Számítsuk ki az integrált definíció szerint:  .
.
Így ez az integrál a-hoz konvergál<1 и расходится при a³1.
3. példa
Vizsgálja meg a konvergenciát ![]() .
.
<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два
 .
.
Az első I1 integrál konvergenciáját az ekvivalens függvénnyel vizsgáljuk: (mivel n>0), és az integrál konvergál m>-1 esetén (2. példa). Hasonlóképpen, az I2 integrál esetében:
És az integrál m+n-ben konvergál<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 és m+n<-1, и будет расходится при нарушении хотя бы одного из них.
4. példa Vizsgálja meg a konvergenciát.
Az integrandus végtelenül nagy lehet (ha m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:
Mivel arctgx »x x®0-nál, az I1 integrál ekvivalens az integrállal, amely m+1>-1, azaz m>-2 esetén konvergál (1. példa).
Az első típusú I2 nem megfelelő integrálban lévő integrandushoz kiválasztunk egy megfelelőt:
![]() mivel arctgx » p/2 at x® ¥. Következésképpen a második összehasonlítási feltétel szerint az I2 integrál m+n-re konvergál<-1, и расходится в противном случае.
mivel arctgx » p/2 at x® ¥. Következésképpen a második összehasonlítási feltétel szerint az I2 integrál m+n-re konvergál<-1, и расходится в противном случае.
Az I1 és I2 integrálok konvergenciájának feltételeit összevonva megkapjuk az eredeti integrál konvergenciájának feltételeit: m>-2 és m+n<-1 одновременно.
Megjegyzés. A 2-4. példákban a 2. összehasonlítási kritériumot alkalmaztuk, amely szükséges és elégséges feltételeket biztosít a konvergenciához, amely lehetővé teszi, hogy a paraméterértékeken valamilyen feltétel mellett konvergenciát állapítottunk meg, hogy ne bizonyítsuk az integrál divergenciáját, ha a kapott konvergencia feltételek teljesülnek. megsértették.
5. példa Vizsgálja meg a konvergenciát.
Ez az integrál egy szinguláris 0 pontot tartalmaz, amelynél az integrandus p-ként mehet a végtelenbe<0, поэтому снова разобьем исходный интеграл на два:
![]() .
.
Az I1 integrál a második típusú nem megfelelő integrál, és az integrandus x®0-nál ekvivalens az xp függvénnyel (e-x®1 x®0-nál), azaz az I1 p>-1-nél konvergál (1. példa).
Az I2 integrál az első típusú nem megfelelő integrál. Nem lehet olyan függvényt kiválasztani, amely ekvivalens az integrandusszal úgy, hogy az ne tartalmazzon exponenciális függvényt. Ezért lehetetlen a 2. összehasonlítási attribútum használata, mint az előző példákban. Alkalmazzuk az első összehasonlítási kritériumot, amelyhez a következő jól ismert tényt használjuk:
![]() A>0 és bármely p. Ebből, és abból, hogy az xpe-ax függvény folytonos, az következik, hogy ez a függvény korlátos, azaz van olyan M>0 állandó, hogy xpe-ax< M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:
A>0 és bármely p. Ebből, és abból, hogy az xpe-ax függvény folytonos, az következik, hogy ez a függvény korlátos, azaz van olyan M>0 állandó, hogy xpe-ax< M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:
Vagyis az I2 integrál bármely p-re konvergál.
Így az eredeti integrál p>-1-nél konvergál.
6. példa Vizsgálja meg a konvergenciát.
Változtassuk meg a változót: t = lnx, és megkapjuk
Az integrál kettéosztását az 5. példához hasonlóan hajtjuk végre. Az I1 integrál teljesen ekvivalens az 5. példa I1 integráljával, ezért q-ban konvergál.<1.
Tekintsük az I2 integrált. Az 1-p<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения ![]() és a=(1-p)/2.).
és a=(1-p)/2.).
Tehát I2 konvergál p>1-re. Ennek az integrálnak a konvergenciájának vizsgálata azonban itt még nem fejeződött be, mivel az alkalmazott konvergenciakritérium csak elegendő feltételeket biztosít a konvergenciához. Ezért tanulmányoznunk kell a konvergenciát 1-p £ 0 esetén.
Tekintsük a p=1 esetet. Ekkor az I2 integrál ekvivalens -vel, ami q>1 esetén konvergál (megjegyzendő, hogy ebben az esetben az I1 integrál divergál), máskülönben pedig divergál.
o<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что ![]() 1-p>0 esetén, és ezért valamilyen A>1-ből kiindulva, T-
KE(1-
P)
T³ M=const>0. Ekkor az I2 integrál kielégíti a becslést
1-p>0 esetén, és ezért valamilyen A>1-ből kiindulva, T-
KE(1-
P)
T³ M=const>0. Ekkor az I2 integrál kielégíti a becslést
 ,
,
Ahol a jobb oldali integrál eltér, ami az I2 integrál divergenciáját bizonyítja.
A kapott eredményeket összegezve azt találjuk, hogy az eredeti integrál q-ban konvergál<1 и p>1, ellenkező esetben az integrál eltér.
6. példa Vizsgálja meg az abszolút és feltételes konvergenciát.
Osszuk ketté az eredeti integrált:
 .
.
Konvergencia. Az I1 integrál ekvivalens  , azaz konvergál a p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.
, azaz konvergál a p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.
Az I2 integrál a Dirichlet-Abel teszt szerint konvergál p>0-ra, mivel az antiderivatív sin(x) korlátos, és az 1/xp függvény monoton nullára hajlik, miközben x a végtelenbe hajlik.
Mutassuk meg, hogy p £ 0 esetén az integrál divergál. Használjuk erre a Cauchy-kritériumot, vagy inkább annak tagadását
 .
.
Vegyük a következő értékeket R1-nek és R2-nek: R1=2pk és R2=2pk+p/2, akkor
 , p>0 esetén.
, p>0 esetén.
Így az integrál 0-hoz konvergál Abszolút konvergencia Az I1 integrál abszolút konvergenciáját már megállapítottuk, tekintsük az I2 abszolút konvergenciáját. Becsüljük meg az integrált felülről: A p £ 1 divergenciájának bizonyításához alulról becsüljük meg az integrált Osszuk fel a függvénykülönbség utolsó integrálját az integrálok különbségére Ha mindkét integrál konvergál, akkor a különbség integrálja konvergál; ha az egyik integrál, a másik pedig konvergál, akkor a különbség integrálja divergál. Mindkét integrál divergenciája esetén a különbség integráljának konvergenciája további vizsgálat tárgyát képezi. Minket a leírt esetek közül a második érdekel. Eltér (1. példa) a p<1. сходится по признаку Дирихле-Абеля при 1>p>0 (lásd Konvergencia), ezért az integrált alulról egy divergens integrál becsüli meg, azaz divergál. A p³1 eset nem érdekel minket, mivel a paraméter ezen értékeinél az integrál eltér. Így az eredeti integrál abszolút 0-hoz konvergál 1. Nem megfelelő integrálok végtelen határértékekkel Emlékezzünk vissza az integrál definíciójára, mint az integrálösszegek határára: A definíció feltételezi, hogy az integrációs intervallum véges, és az f(x) függvény folytonos benne. Ezen feltevések megsértése helytelen integrálokhoz vezet. Meghatározás. Ha az integrál véges határra hajlik, ahogy korlátlanul növekszik "b", akkor ezt a határértéket nem megfelelő integrálnak nevezzük az f (x) függvény végtelen felső határával, és a szimbólummal jelöljük Ebben az esetben azt mondjuk, hogy a nem megfelelő integrál létezik, vagy konvergál. Ha a megadott határérték nem létezik, vagy létezik, de végtelen, akkor azt mondjuk, hogy az integrál nem létezik, vagy eltér. A végtelen alsó korláttal rendelkező helytelen integrált hasonlóan definiáljuk: Egy két végtelen határú nem megfelelő integrált a következőképpen adunk meg: ahol c az Ox tengely bármely fix pontja. Tehát a nem megfelelő integráloknak lehet végtelen alsó korlátja, végtelen felső korlátja és két végtelen korlátja is. Integrál csak akkor létezik, ha mindegyik integrál létezik: és . Példa. Vizsgáljuk meg az integrál konvergenciáját! Feltéve, hogy c = 0, a következőt kapjuk: azok. az integrál konvergál. Néha nincs szükség helytelen integrál kiszámítására, elég csak annyit tudni, hogy konvergál vagy divergál, ha összehasonlítjuk egy másik integrállal. Legyen az f (x) függvénynek az intervallumban több első típusú (véges számú) szakadási pontja, ez az „akadály” könnyen kiküszöbölhető, ha a szakaszt több szakaszra osztjuk szakadási pontokkal, meghatározott integrálokat számítunk minden egyes szakaszon és az eredményeket összeadva. Tekintsük egy függvény határozott integrálját, amely korlátlan, amikor a szegmens valamelyik végéhez közelítünk, pl. (Ilyenkor általában azt mondják: "A függvénynek végtelen szakadása van az integrációs intervallum jobb végén".) Nyilvánvaló, hogy az integrál szokásos meghatározása itt értelmét veszti. Meghatározás. Az f(x) függvény nem megfelelő integrálja, folytonos £ x esetén< b и неограниченной при x ® b - 0, называется предел: A szegmens bal végén végtelen szakadást mutató függvény nem megfelelő integrálját hasonlóan definiáljuk: Következésképpen a [-1, 0] szakaszban az integrál divergál. Ez azt jelenti, hogy az integrál is divergál a szakaszban. Így ez az integrál a teljes intervallumban divergál [-1, 1]. Vegyük észre, hogy ha ezt az integrált úgy kezdenénk kiszámolni, hogy nem figyelnénk az integrandus szakadásra az x = 0 pontban, akkor hibás eredményt kapnánk. Igazán, Tehát egy nem folytonos függvény nem megfelelő integráljának tanulmányozásához több integrálra kell „felosztani” és tanulmányozni azokat. Mint tudják, az integrál megtalálása meglehetősen nehéz feladat lehet. Nagy csalódás lenne, ha elkezdenénk kiszámolni egy nem megfelelő integrált, és az út végén azt találnánk, hogy az eltér. Ezért érdekesek azok a módszerek, amelyek lehetővé teszik, hogy egyetlen függvénytípuson alapuló komoly számítások nélkül következtetéseket vonjunk le egy nem megfelelő integrál konvergenciájára vagy divergenciájára. Az alábbiakban tárgyalandó első és második összehasonlító tétel nagyban segíti a konvergencia helytelen integráljainak tanulmányozását. Legyen f(x)?0. Aztán a funkciókat monoton növekszik a t vagy -g változókban (mivel g>0-t veszünk, a -g balról nullára hajlik). Ha az argumentumok növekedésével az F 1 (t) és F 2 (-d) függvény felülről korlátos marad, ez azt jelenti, hogy a megfelelő nem megfelelő integrálok konvergálnak. Ez az alapja a nemnegatív függvények integráljaira vonatkozó első összehasonlítási tételnek. Legyen az f(x) és g(x) függvény x?a-ban teljesítse a következő feltételeket: Ekkor az integrál konvergenciájából az integrál konvergenciája következik, az integrál divergenciájából pedig a divergencia Mivel 0?f(x)?g(x) és a függvények folytonosak, akkor Feltétel szerint az integrál konvergál, azaz. véges értéke van. Ezért az integrál is konvergál. Most hagyjuk, hogy az integrál divergáljon. Tegyük fel, hogy az integrál konvergál, de akkor az integrálnak konvergálnia kell, ami ellentmond a feltételnek. Feltevésünk téves, az integrál eltér. Összehasonlítási tétel a 2. típusú nem megfelelő integrálokra. Legyen az intervallum f(x) és g(x) függvényei korlátlanul növelve x>+0 esetén. x>+0 esetén a következő egyenlőtlenség érvényesül:<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также. Összehasonlítási tétel 1. típusú nem megfelelő integrálokra. Legyen az f(x) és g(x) függvény a $ intervallumon, hogy mindkét alábbi számot végesnek tételezzük fel. Ha csak 1 megszakítás van, akkor az $a$ pontban, vagy $b$ pontban, vagy a $(a,\,b)$ intervallumon belül lehet. Tekintsük először azt az esetet, amikor $a$ pontban van egy második típusú szakadás, a többi pontban pedig folytonos az integrandusfüggvény. Tehát az integrálról beszélünk \begin(egyenlet) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(egyenlet) és $f(x) \rightarrow \infty $, amikor $x \rightarrow a+0$. Mint korábban, először is értelmet kell adni ennek a kifejezésnek. Ehhez vegye figyelembe az integrált \[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \] Meghatározás. Legyen véges határ \[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \] Ekkor a második típusú (22) nem megfelelő integrálról azt mondjuk, hogy konvergál, és hozzárendeljük a $A$ értéket; magát a $f(x)$ függvényt pedig integrálhatónak mondjuk a $\left[ a, \ intervallumban. , b\right]$. Tekintsük az integrált \[ I=\int ^1_0\frac(dx)(\sqrt(x)). \] A $1/\sqrt(x)$ integrand függvénynek a $x \rightarrow +0$ pontban végtelen határa van, tehát a $x=0$ pontban másodlagos folytonossági hiánya van. Tegyük fel \[ I(\epsilon)=\int ^1_(\epsilon )\frac(dx)(\sqrt(x))\,. \] Ebben az esetben az antiderivatív ismert, \[ I(\epsilon)=\int ^1_(\epsilon )\frac(dx)(\sqrt(x))=2\sqrt(x)|^1_(\epsilon )=2(1-\sqrt( \epsilon ))\jobbra nyíl 2\] at $\epsilon \rightarrow +0$. Így az eredeti integrál egy második típusú konvergens nem megfelelő integrál, és egyenlő 2-vel. Tekintsük azt a lehetőséget, amikor az integrandusfüggvényben az integrációs intervallum felső határán másodlagos folytonossági hiány van. Ez az eset a $x=-t$ változó változtatásával, majd az integráció határainak átrendezésével redukálható az előzőre. Tekintsük azt a lehetőséget, amikor az integrandus függvénynek van egy második típusú szakadása az integrációs intervallumon belül, a $c \in (a,\,b)$ pontban. Ebben az esetben az eredeti integrál \begin(egyenlet) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(egyenlet) összegként mutatják be \[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \] Meghatározás. Ha mindkét $I_1, \, I_2$ integrál konvergál, akkor a nem megfelelő integrált (23) konvergensnek nevezzük, és a $I_1, \, I_2$ integrálok összegével egyenlő értéket kap, a $f(x)$ függvényt. integrálhatónak nevezzük a $\left [a, \, b\right]$ intervallumban. Ha a $I_1,\, I_2$ integrálok közül legalább az egyik divergens, a (23) nem megfelelő integrált divergensnek nevezzük. A 2. típusú konvergens nem megfelelő integrálok a közönséges határozott integrálok összes standard tulajdonságával rendelkeznek. 1. Ha $f(x)$, $g(x)$ integrálható a $\left[ a, \,b \right ]$ intervallumban, akkor ezek összege $f(x)+g(x)$ ezen az intervallumon is integrálható, és \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Ha a $f(x)$ integrálható a $\left[ a, \, b \right ]$ intervallumban, akkor bármely $C$ konstans esetén a $C\cdot f(x)$ függvény is integrálható ezen az intervallumon , és \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Ha a $f(x)$ integrálható a $\left[ a, \, b \right ]$ intervallumban, és ezen az intervallumon a $f(x)>0$, akkor \[ \int _a^ (b ) f(x)dx\,>\,0. \] 4. Ha $f(x)$ integrálható a $\left[ a, \, b \right ]$ intervallumban, akkor bármely $c\in (a, \,b)$ esetén a \[ \ integrálok int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] szintén konvergál, és \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (az integrál összeadódása az intervallumon belül).
Tekintsük az integrált \begin(egyenlet) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(egyenlet) Ha $k>0$, az integrandus általában $\infty$, mint $x \rightarrow +0$, tehát az integrál nem megfelelő a második fajtából. Bemutatjuk a függvényt \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \] Ebben az esetben az antiderivatív ismert, tehát \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \] $k \neq 1$-ért, \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \] ha $k = 1$. Figyelembe véve a $\epsilon \rightarrow +0$ viselkedését, arra a következtetésre jutunk, hogy a (20) integrál $k pontban konvergál Tétel (az összehasonlítás első jele). Legyen $f(x)$, $g(x)$ folytonos $x\in (a,\,b)$ és $0 1 esetén. Ha a \[ \int _a^(b)g(x) integrál dx \] konvergál, akkor a \[ \int _a^(b)f(x)dx integrál konvergál. \] 2. Ha a \[ \int _a^(b)f(x)dx \] integrál eltér, akkor a \[ \int _a^(b)g(x)dx integrál divergál. \] Tétel (második összehasonlítási kritérium). Legyen $f(x)$, $g(x)$ folytonos és pozitív $x\in (a,\,b)$ esetén, és legyen véges határ \[ \theta = \lim_(x \jobbra nyíl a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \] Aztán az integrálok \[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \] egyidejűleg konvergálnak vagy divergálnak. Tekintsük az integrált \[ I=\int _0^(1)\frac(1)(x+\sin x)\,dx. \] Az integrandus egy pozitív függvény az integrációs intervallumon, az integrandus általában $\infty$, mint $x \rightarrow +0$, tehát az integrálunk egy második típusú nem megfelelő integrál. Továbbá $x \rightarrow +0$ esetén a következőt kapjuk: ha $g(x)=1/x$, akkor \[ \lim _(x \jobbra nyíl +0)\frac(f(x))(g(x))=\lim _(x \jobbra nyíl +0)\frac(x)(x+\sin x)=\ frac(1)(2) \neq 0,\, \infty \, . \] A második összehasonlítási feltételt alkalmazva arra a következtetésre jutunk, hogy az integrálunk az integrállal egyidejűleg konvergál vagy divergál. \[ \int _0^(+1)\frac(1)(x)\,dx . \] Ahogy az előző példában is látható volt, ez az integrál divergál ($k=1$). Következésképpen az eredeti integrál is eltér. Számítsa ki a nem megfelelő integrált, vagy állapítsa meg a konvergenciáját (divergenciáját). 1. \[ \int _(0)^(1)\frac(dx)(x^3-5x^2)\,. \] 2. \[ \int _(3)^(7)\frac(x\,dx)((x-5)^2)\,. \] 3. \[ \int _(0)^(1)\frac(x\,dx)(\sqrt(1-x^2))\,. \] 4. \[ \int _(0)^(1)\frac(x^3\,dx)(1-x^5)\,. \] 5. \[ \int _(-3)^(2)\frac(dx)((x+3)^2)\,. \] 6. \[ \int _(1)^(2)\frac(x^2\,dx)((x-1)\sqrt(x-1))\,. \] 7. \[ \int _(0)^(1)\frac(dx)(\sqrt(x+x^2))\,. \] 8. \[ \int _(0)^(1/4)\frac(dx)(\sqrt(x-x^2))\,. \] 9. \[ \int _(1)^(2)\frac(dx)(xlnx)\,. \] 10. \[ \int _(1)^(2)\frac(x^3\,dx)(\sqrt(4-x^2))\,. \] 11. \[ \int _(0)^(\pi /4)\frac(dx)(\sin ^4x)\,. \] Az első típusú nem megfelelő integrálok. Lényegében ez ugyanaz a határozott integrál, de azokban az esetekben, amikor az integráloknak végtelen felső vagy alsó integrációs határa van, vagy mindkét integrálási határ végtelen. A második típusú nem megfelelő integrálok. Lényegében ez ugyanaz a határozott integrál, de azokban az esetekben, amikor az integrált korlátlan függvényekből vesszük, a véges számú pontban lévő integrandusnak nincs véges integrálási szegmense, amely végtelenbe fordul. Összehasonlításképp. A határozott integrál fogalmának bevezetésekor azt feltételeztük, hogy a függvény f(x) folyamatos a [ a, b], és az integrációs szegmens véges, azaz számok korlátozzák, és nem a végtelen. Egyes feladatok e korlátozások feladásához vezetnek. Így jelennek meg a nem megfelelő integrálok. A nem megfelelő integrál geometriai jelentése Egészen egyszerűen kiderül. Abban az esetben, ha egy függvény grafikonja y = f(x)
a tengely felett van Ökör, a határozott integrál egy görbével határolt görbe vonalú trapéz területét fejezi ki y = f(x)
, x tengely és ordináták x = a
, x = b. A nem megfelelő integrál viszont egy korlátlan (végtelen) görbe vonalú trapéz területét fejezi ki, amely a vonalak közé van zárva y = f(x)
(az alábbi képen - piros), x = aés az abszcissza tengely. A helytelen integrálokat hasonlóképpen határozzuk meg más végtelen intervallumokhoz: Egy végtelen görbe trapéz területe lehet véges szám, ebben az esetben a nem megfelelő integrált konvergensnek nevezzük. A terület lehet végtelen is, és ebben az esetben a nem megfelelő integrált divergensnek nevezzük. Egy integrál határértékének használata a nem megfelelő integrál helyett. A nem megfelelő integrál kiértékeléséhez a határértéket kell használni határozott integrál. Ha ez a határ létezik, és véges (nem egyenlő a végtelennel), akkor a nem megfelelő integrált konvergensnek, egyébként pedig divergensnek nevezzük. Az, hogy egy változó milyen mértékben hajlik a határjel alá, attól függ, hogy az első vagy a második típusú nem megfelelő integrállal van-e dolgunk. Tudjunk erről most. Tehát egy nem megfelelő integrál írása abban különbözik a szokásos határozott integráltól, hogy az integráció felső határa végtelen. Meghatározás. Nem megfelelő integrál egy folytonos függvény integrálásának végtelen felső határával f(x)
közötti intervallumban a
előtt ∞
ennek a függvénynek az integráljának határát az integráció felső határával nevezzük b
és az integráció alsó határa a
feltéve, hogy az integráció felső határa korlátlanul nő, azaz Ha ez a határ létezik, és nem a végtelen, hanem valamilyen számmal egyenlő, akkor a nem megfelelő integrált konvergensnek nevezzük, és azt a számot veszik értéknek, amellyel a határ egyenlő. Másképp a nem megfelelő integrált divergensnek nevezzükés semmi értelmet nem tulajdonítanak neki. Példa 1. Számítsa ki a nem megfelelő integrált(ha összefolyik). Megoldás. A nem megfelelő integrál definíciója alapján azt találjuk Mivel a határ létezik és egyenlő 1-gyel, akkor ez helytelen integrál konvergálés egyenlő 1-gyel. A következő példában az integrandus majdnem ugyanaz, mint az 1. példában, csak az x fok nem kettő, hanem az alfa betű, és a feladat a nem megfelelő integrál tanulmányozása a konvergenciához. Vagyis a kérdés megválaszolásra vár: milyen alfa-értékeknél konvergál ez a helytelen integrál, és milyen értékeknél tér el? 2. példa Vizsgálja meg a nem megfelelő integrált a konvergenciára(az integráció alsó határa nagyobb, mint nulla). Megoldás. Akkor először tegyük fel, hogy Az eredményül kapott kifejezésben a következő határértékre lépünk: Könnyen belátható, hogy a jobb oldali határ létezik, és egyenlő nullával, amikor , vagyis amikor nem létezik, azaz . Az első esetben, amikor . Ha akkor Tanulmányunk következtetése a következő: ez helytelen integrál konvergálés eltér nál nél . A Newton-Leibniz képlet alkalmazása a vizsgált nem megfelelő integrál típusára Ez egy általánosított Newton-Leibniz képlet. 3. példa: Számítsa ki a nem megfelelő integrált(ha összefolyik). Ennek az integrálnak a határa létezik: A második integrál, amely az eredeti integrált kifejező összeget alkotja: Ennek az integrálnak a határa is létezik: Megtaláljuk két integrál összegét, ami egyben az eredeti nem megfelelő integrál értéke is két végtelen határral: Hagyja a függvényt f(x)
tól származó szegmensen adott a
előtt b
és korlátlan. Tegyük fel, hogy a függvény a pontban a végtelenbe megy b
, míg a szakasz összes többi pontján folytonos. Meghatározás. Egy függvény nem megfelelő integrálja f(x)
től származó szegmensen a
előtt b
ennek a függvénynek az integráljának határát az integráció felső határával nevezzük c
, ha a törekvés során c
Nak nek b
a függvény korlátozás nélkül növekszik, és a ponton x = b
funkció nincs definiálva, azaz Ha ez a határ létezik, akkor a második típusú nem megfelelő integrált konvergensnek, ellenkező esetben divergensnek nevezzük. A Newton-Leibniz képlet segítségével levezetjük. , azaz az integrál konvergál p>1 esetén.
, azaz az integrál konvergál p>1 esetén. .
. .
.



A konvergencia jelei. Abszolút és feltételes konvergencia

Nem megfelelő integrálok összehasonlító tétele.
![]() .
.


 , ami lehetetlen.
, ami lehetetlen.![]()
10.2.2 Tesztek a 2. típusú nem megfelelő integrálok konvergenciájára

Az első típusú helytelen integrálok - végtelen határokkal és konvergenciájukkal
Nem megfelelő integrálok végtelen felső határral
![]() .
.

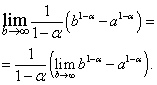
 és nem létezik.
és nem létezik.![]() , levezetheti a következő képletet, amely nagyon hasonlít hozzá:
, levezetheti a következő képletet, amely nagyon hasonlít hozzá: .
.![]()

![]() .
.A második típusú helytelen integrálok - korlátlan függvényekből és konvergenciájukból
![]() .
.